Füst elvárással (sor)
Ahogy teljesítménymutatók QS várakozással mellett a már ismert teljesítmény - abszolút és relatív sávszélesség, a kudarc valószínűsége, az átlagos elfoglalt csatornák (többcsatornás rendszer) is figyelembe kell venni a következőket:
1) - az alkalmazások átlagos száma a rendszerben;
2) - az alkalmazási idő átlagos időtartama a rendszerben;
3) - a sorban szereplő kérések átlagos száma (sor hossz);
4) - a várakozási idő átlagos alkalmazási ideje;
5) - annak valószínűsége, hogy a csatorna foglalt (a csatorna terhelése).
Egycsatornás rendszer korlátlan sorban
Van egy egycsatornás SMO várakozási sorral, amely nincs korlátozva (sem várólistán, sem várakozási időn kívül). Az SMO-ba érkező alkalmazások áramlása intenzitással bír, és a szolgáltatás áramlása intenzitással bír. Szükséges megtalálni a QS korlátozó valószínűségeit és teljesítménymutatóit.
A rendszer a következő állapotok valamelyikében lehet az SMS-ben lévő alkalmazások száma szerint: - a csatorna szabad; - a csatorna foglalt (ez az alkalmazást szolgálja), nincs sor; - a csatorna foglalt, egy alkalmazás a sorban van; - a csatorna elfoglalt, a megrendelések várakoznak, stb.
A QS állapotok grafikonját az 1. ábra mutatja. 8.
Ez egy halálozási és szorzási folyamat, de végtelen számú olyan állapotban, amelyben az alkalmazások áramlási intenzitása egyenlő, és a szolgáltatás áramlásának intenzitása.
Mielőtt leírná a maximális valószínűségű képleteket, meg kell győződnie arról, hogy létezik, mert abban az esetben, ha az idő, a sor korlátozás nélkül növelhető. Bizonyítottam, hogy ha, azaz. a beérkező alkalmazások átlagos száma kisebb, mint a kiszolgált kérések átlagos száma (időegységenként), akkor léteznek korlátozó valószínűségek. Ha a sor végére nő.
Annak megállapításához, a marginális valószínűségi állapotok használja a képlet (16), (17) a születés és halál folyamata (itt feltételezzük, bizonyos mértékű hiánya a szigor, mint korábban, ezek a képletek alapján készültek esetén véges sok állapot a rendszer). Kapunk:
8. példa A kikötőnek egy hajóhelye van a hajók kirakodására. Az edények áramlási intenzitása 0,4 (hajó naponta). Az átlagos hajózási idő hajónként 2 nap. Feltételezzük, hogy a sor vége lehet korlátlan hossza. Keresse meg a kikötő teljesítménymutatóit, valamint azt a valószínűséget, hogy a kirakodás várakozásai nem haladják meg a 2 hajót.
A megoldás. Van. Azóta a kirakodási sor nem növekszik a végtelenségig, és marginális valószínűségek léteznek. Találjuk meg őket.
Annak a valószínűsége, hogy a kikötőhely szabad (33) szerint, de annak valószínűsége, hogy elfoglalt. A (34) képlet szerint az 1, 2, 3 hajó (vagyis a 0, 1, 2 hajó ürítésének várakozása)
Annak a valószínűsége, hogy legfeljebb két hajó kiürítését várják
A (40) képlet szerint a kirakodásra váró hajók átlagos száma, a (42) (nap) képlet szerinti ürítés átlagos várakozási ideje.
A képlet szerint (36) az átlagos száma horgonyzó hajók (nap) (vagy egyszerűbb (37) (nap), és az átlagos tartózkodási idő a hajó a Pier amelyet a képlet (41) (nap).
Nyilvánvaló, hogy a hajók kirakodásának hatékonysága alacsony. Ennek növelése érdekében csökkenteni kell a hajó kirakodásának átlagos időtartamát, vagy növelni kell a kikötők számát.
Többcsatornás SMO korlátlan sorban
Fontolja meg a problémát. Van egy n-csatornás SMO, korlátlan sorral. Az SMO-ba érkező alkalmazások áramlása intenzitással bír, és a szolgáltatás áramlása intenzitással bír. Meg kell találni a KHSZ állapotok korlátozó valószínűségét és hatékonysági mutatóit.
A rendszer az egyik állapotban lehet, amelyet a QMS-ben található alkalmazások száma számoz: - nincsenek alkalmazások a rendszerben (minden csatorna szabad); - egy csatorna elfoglalt, a többi szabad; - két csatorna foglalt, a többi szabad; - elfoglalt csatornák, a többiek ingyenesek; - minden csatorna foglalt (nincs várakozási sor); - minden csatorna foglalt, egy alkalmazás a sorban; - minden csatorna foglalt, a megrendelések sorban vannak, stb.
A rendszerállapotok grafikonját az 1. ábra mutatja. 9. Tudomásul vesszük, hogy ellentétben a korábbi QS intenzitás fluxus karbantartás (átviszi a rendszer egyik állapotból a másikba, jobbra) nem marad állandó, hanem az alkalmazások száma a QS 0-ról a nagysága, hogy már ennek megfelelően nő a szolgáltatási csatornák száma. A QMS-ben lévő alkalmazások számával nagyobb, mint a szervizmennyiség intenzitása.
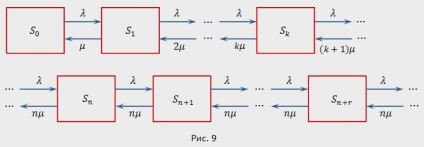
Megmutatható, hogy a valószínűségek korlátozására léteznek. Ha a sor végére nő. A képletek (16) és (17) a születés és halál folyamat, mi állíthatjuk elő az alábbi képletet a marginális valószínűségek államok n-csatornás QS korlátlan sorban
Az átlagos tartózkodási idő a kérelem várakozási sor, és az átlagos tartózkodási idő az alkalmazás rendszer, mint korábban, által adott Kis (42) és (41).
Megjegyzés. A QMS korlátlan sorral, minden olyan alkalmazás esetében, amely belépett a rendszerbe, az kiszolgálásra kerül, azaz a hiba valószínűsége, a relatív áteresztőképesség és az abszolút kapacitás megegyezik az alkalmazások bejövő áramlási intenzitásával, azaz. .
9. példa A szupermarketben az ügyfél intenzitással érkezik a település csomópontjába. óránként. Átlagos szervizidő egy ügyfel pénztár-vezérlőjével min. meghatározni:
a. A minimális számú vezérlő, pénztáros, amelyben a sor nem fog nőni a végtelenségig, és a megfelelő szolgáltatási jellemzők mikor.
a. Az a valószínűség, hogy a várólistában nem lesz több három ügyfél.
A megoldás. a. Az állapot (1 / h) (1 / perc). A (24) képlet segítségével. A sor nem növekszik a végtelenig, feltéve, hogy - azaz a \ rho = 2, \! 7 "src =" http://www.bourabai.kz/cm/waiting_sys/mathtex(82).gif „>. Így a minimális számát vezérlők-pénztárosok.
Nézzük meg a QMS szolgáltatás jellemzőit.
Annak a valószínűsége, hogy a települési csomópontban nincsenek vásárlók a (45) képlet szerint,
azaz átlagosan 2,5% -a, a pénztárosok készenlétben maradnak.
Annak a valószínűsége, hogy a számítási csomópontban a (48)
A várakozók átlagos száma (50)
A várakozás és a jegyvásárlás átlagos időtartama megegyezik (a (42) és (41) képletek szerint):
A második változatban két egycsatornás SMO (két speciális ablak) van; mindegyikük erőteljesen fogadja az alkalmazások áramát. Mint korábban, léteznek korlátozó valószínűségek. A (40), (36), (42), (41)
Tehát a második változat szerint a várakozási idő és az átlagos várakozási idő, valamint általában a jegyek vásárlása nőtt. Ez a különbség azzal a ténnyel magyarázható, hogy az első kiviteli (kétcsatornás SMO) kevesebb, mint az átlagos százalékos aránya tétlen az egyik szavazatszámláló, ha nem foglalt szervizelése utas vásárol jegyet a lényeg, ő tehet szolgáltatás utas, aki vásárol jegyet egy pont, és fordítva . A második változatban nincs ilyen felcserélhetőség.
Megjegyezzük, hogy a jegyvásárlás átlagos időtartama a második opciónál több mint 2 alkalommal nőtt. Az ilyen jelentős növekedés annak a ténynek köszönhető, hogy az SMO a lehetőségeinek határán dolgozik: elegendő az átlagos szolgáltatási idő némileg növelni, pl. csökkenti és meghaladja az 1-et, azaz. a sor elején korlátlanul növekszik.
b. Megállapítást nyert, hogy a jegyértékesítés első változata szerint egy átlagos utasidő (min.) Átlagos üzemideje alapján a jegyek vásárlásának átlagos ideje (min). A második értékesítési lehetőség vagy a (36) és (41) figyelembevételével:.
Feltéve, hogy megtaláljuk, ahol találunk vagy (min).
Így az eladások második változata szerinti jegyvásárlásra fordított átlagos idő csökken, ha az utasok átlagos szolgálati ideje 0,17 percnél, vagy több mint 8,5% -kal csökken.
SMO korlátozott sorral
A korlátozott sorral rendelkező QSO-k eltérnek a fent tárgyalt feladatoktól, csak abban az esetben, ha a sorban lévő alkalmazások száma korlátozott (nem haladhatja meg a megadott értékeket). Ha az új alkalmazás abban a pillanatban érkezik meg, amikor a sorban lévő összes hely elfoglalt, akkor az SMO el nem hagyott, vagyis nem. visszautasítást kap.
Nyilvánvaló, hogy a számítási korlátozása valószínűségek az államok és a hatékonyság ilyen SMO lehet használni ugyanazt a megközelítést, mint fent, azzal a különbséggel, hogy összefoglalják nem kell végtelen progresszió (ahogy tettük a levezetése (33) képletű), és a végső . A megfelelő képleteket a táblázatban foglaljuk össze. 3.
Az alkalmazásnak a sorban és a rendszerben maradt átlagos időtartamát a korábbiakhoz hasonlóan a kis képletek (44) és (43) határozzák meg.
11. példa A 8. példában feltüntetett körülmények között keresse meg a kikötő teljesítménymutatóit. Ismeretes, hogy a bejövő hajó elhagyja a mólót (kirakodás nélkül), ha több mint 3 hajó van a sorban a kirakodáshoz.
A megoldás. A feltétellel. A táblázat második oszlopában megadott képleteket használjuk. 3.
Annak a valószínűsége, hogy a horgonyzás ingyenes:
Annak a valószínűsége, hogy a bejövő hajó kirakodás nélkül elhagyja a kikötőt:
A hajók átlagos száma a horgonyzóhelyen, valamint a hajó tartózkodási ideje a hajóágyon (41) szerint:
Időzített QMS
A gyakorlatban a KKT-k gyakran találkoznak az úgynevezett "türelmetlen" alkalmazásokkal. Az ilyen kérelmek elhagyhatják a sorokat, ha a várakozási idő meghalad egy bizonyos értéket. Különösen ez a fajta alkalmazás felmerülő különböző technológiai rendszerek késleltetheti a szolgáltatás elvesztését eredményezheti a minőségi termékek, a működési rendszerek, amikor sürgős üzenetek elveszti az értékét (vagy értelme), ha azok nem a szolgáltatás egy bizonyos időben.
Az ilyen rendszerek legegyszerűbb matematikai modelljeiben azt feltételezzük, hogy az alkalmazás véletlenszerű időben véletlen sorrendben, az exponenciális törvény szerint osztható el bizonyos paraméterekkel, azaz pl. feltételesen feltételezhetjük, hogy minden olyan alkalmazás, amely a karbantartás során várakozik, a rendszer intenzitással hagyhatja el.
A korlátozott időtartamú QS megfelelő teljesítménymutatóit a halálozási és reprodukciós folyamat eredményei alapján kapják meg.
Végezetül megjegyezzük, hogy a gyakorlatban gyakran vannak zárt rendszerű szolgálatok. amelyben az alkalmazások bejövő áramlata jelentősen függ a KPSZ állapotától. Példaként egy olyan helyzetben, ahol javítási lehetőség a területen működésének néhány az autók: egyértelmű, hogy minél több gép egy állapotban, annál kevésbé továbbra is használnak, és minél alacsonyabb a folyamat intenzitása az új belépők a javítás gép. A zárt QMS-hez korlátozott számú alkalmazásforrás van jellemző, minden forrás "blokkolt" az alkalmazás szervizelésének ideje alatt (azaz nem ad ki új alkalmazásokat). Az ilyen rendszerekben, az SMO állapotok véges számú számára, a korlátozó valószínűségek léteznek az alkalmazásáramok intenzitásának és a karbantartásnak bármely értékére vonatkozóan. Ezek kiszámíthatók a halál és a reprodukció folyamatában.
Tudta-e, hogy egy algoritmus egy sor utasítás, amely leírja a művész intézkedéseinek sorrendjét, hogy elérje a probléma megoldásának eredményét véges számú cselekvésre. A régi értelmezésben a "rend" szó helyett a "szekvencia" szót használták, de a számítógépes munkában a párhuzamosság fejlődésével a "szekvencia" szót az általánosabb "rend" szó váltotta fel. Ez annak köszönhető, hogy az algoritmus egyes utasításainak működése függhet más utasításoktól vagy munkájuk eredményétől. Így néhány utasítást szigorúan végre kell hajtani az utasítások befejezése után, amelyről függenek. Független utasításokat vagy utasításokat, amelyek az utasítások befejezésétől függetlenül függetlenek, párhuzamosan vagy egyidejűleg, véletlenszerű sorrendben, ha a használt processzor és az operációs rendszer lehetővé teszik.
HÍREK A FORUM
Az éter elméletének lovagjai