Kúpos szakasz
Kúpszelet. vagy a kúp [1]. - egy sík metszete egy kör alakú kúppal. A kúpos szakaszok három fő típusa van: egy ellipszis. parabola és hiperbola. ezen kívül vannak degenerált szakaszok is: egy pont. Egyenes és egy pár egyenes vonal. A kör egy ellipszis különleges esetének tekinthető.
A kúp alakú szakaszok egy sík metszéspontjával nyithatók meg, kétoldalú kúppal
Ha a gép áthalad a származáson. akkor egy degenerált szakaszt kapunk. A nemkívánatos esetben,
- Ha a secant sík metszi az összes kúp generátort az egyik üregének pontjaiban, ellipszist kapunk,
- Ha a szekvencia sík párhuzamos a kúp érintő síkjával, akkor parabárt kapunk,
- Ha a szekvencia sík metszi a kúp mindkét kavitját, kapunk egy hiperbolt.
Az egyenlet a kör alakú kúpos négyzet, ezért minden kúpszelet szakaszok Quadrics. és minden négyzetes síkban vannak kúpszeletek (bár két párhuzamos vonal képez degenerált quadric, amelyet nem lehet kapjuk a kúp részben, de még mindig általában úgy, hogy „degenerált kúpszelet”).
A kúpos szakaszokat az ókori Görögország matematikusai ismerték.
Ezeknek a görbéknek a legteljesebb kompozíciója az Apollonius of Perga (Kr. E. 200) "kúpos része" volt. Nyilvánvalóan ő volt az első, aki leírta az ellipszis és a hiperbola gerincét [2]: 41.
Papp Alexandria először a parabola fókuszát írta le, és a pontok helyére általános összefüggést kapott a kúpszakasz számára. amelyhez a távolságok és a direktrix közötti távolság állandó [2]: 48.
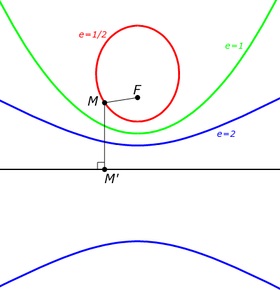
Ellipszis (e = 1/2). parabola (e = 1) és hiperbola (e = 2) fix fókusszal F és direktrix.
Minden nem degenerált kúpos szakasz, a kör kivételével. a következőképpen írható le:
Választhatunk egy F pontot a síkban és egy egyenes vonalat d, és meghatároznunk egy valós számot e ≥ 0. Ezután a pontok helyszíne. amelyre az F ponttól a d vonalig terjedő távolság különbözik az e tényezőtől, kúpszelet. Az F pontot a kúpszakasz fókuszának nevezzük, és a d vonal a direktrix. az e szám az excentricitás.
Az excentricitástól függően kiderül:
Az excentricitás kapcsolódik a kúp paramétereihez és a vágó sík helyehez a kúp tengelyéhez viszonyítva az alábbi összefüggéssel [3]: 46.47:
Itt ψ - szöget zár be a vágási sík a kúp tengelye, φ - közötti szög alkotó és a tengely a kúp felével egyenlő a kúp szöge. Ebből a képletből látható, hogy a kúp metsző síkja állíthatók elő bármilyen excentricitás ellipszis, parabola, hiperbola, és csak akkor kapunk oly módon, hogy az excentricitás nem több, mint 1 cos φ >>. Ez a maximum érték elérésekor egy adott keresztmetszetben a kúpot egy párhuzamos síkban a tengelye körül.
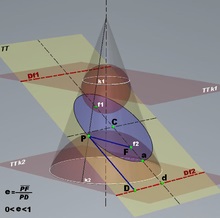
Ellipszis (kék), mint kúpos szakasz, amely elválasztja a Dandelen golyókat; az ellipszis (Df1 és Df2), a fókuszai (f1 és f2) és az excentricitás (e)
A kúpos szakaszok fontos tulajdonságait a kúpszakaszhoz és a kúphoz (Dandelen golyókhoz) tartozó két golyó figyelembe vételével érhetjük el. Például segítségükön keresztül a kúpszakasz fókuszának, direktrixének és excentricitásának mértani jelentése meg van határozva [3]: 46,47.
- A síkon lévő öt ponton keresztül, amelyek közül három nem egy vonalon fekszik, egyetlen kúpos szakaszt húzhat meg.
- Két nondegenerált kúp alakú excentricitása egybeesik akkor, ha és csak akkor, ha hasonlóság-transzformációval lefordíthatók egymásba.
- Az affin transzformációk csak az excentricitás jeleit tartják meg, azaz az affin geometria szempontjából csak három különböző nem degenerált kúpos szakasz van: egy ellipszis, egy parabola és egy hiperbola.
- Minden nem-elvágott kúp alakú szakasz a projektív geometriában megkülönböztethetetlen.
Descartes-koordináták
A x 2 + B x y + C y 2 + D x + E y + F = 0. + Bxy + Cy ^ + Dx + Ey + F = 0,>
meghatározza a kúpszakasz típusát.
- Ha a diszkriminancia kisebb mint nulla, akkor ez ellipszis. pont vagy üres készlet.
- Ha a diszkriminancia nulla, akkor ez egy parabola. Egyenes vagy pár párhuzamos egyenes vonal.
- Ha a diszkrimináns nullánál nagyobb, akkor ez egy hiperbola vagy egy pár metszővonal
Poláris koordináták
Poláris koordinátákban (ρ. Θ). ahol a középpont az egyik fókuszban és a nulla tengely mentén a fő tengely mentén, a kúpszakaszt az egyenlet képviseli
ahol e jelöli az excentricitást, és l állandó.
A klasszikus mechanika, a pálya szabad mozgásának gömb alakú tárgyak egy vákuum alá egy alkalmazást, az inverz négyzetes törvény - az egyetemes tömegvonzás törvénye. és ezért az egyik ferde görbe - egy parabola, hiperbola, ellipszis, vagy egy egyenes vonal. Bolygók pályájának - az ellipszis pályához üstökösök - ellipszis alakú, hiperbolák [4] vagy „majdnem parabolikus” [5] (lásd még Celestial Mechanics.) Repülési útvonal kapura kivételével levegő hatása - ellipszis ív (lásd még a ballisztikai.).