A parabola szegmens kvadratúrája - stadopedia
A készítményben Quadrature parabola Archimedes bebizonyította, hogy a terület egy szegmensét egy parabola, a lehallgatott a vonal ez a téren írva a háromszög szegmens (lásd. Ábra).
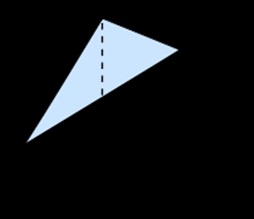
A bizonyítás érdekében Archimédész számította ki egy végtelen sorozatot:
A sorozatok mindegyike a sorozat előző tagjai által nem fedett parabola szegmens szegmensében szereplő háromszögek teljes területét jelenti.
Amellett, hogy a fenti, Archimedes számított felület egy gömb szegmens és kapcsolja őket nyitott „archimedesi spirál”, meghatározott térfogatú labdát szegmensek egy ellipszoid, paraboloid és hiperboloid két lap forgási.
A következő probléma a görbék geometriájával kapcsolatos.
Adjon egy görbét. Hogyan lehet meghatározná a tangent bármely pontján? Vagy ha ezt a problémát a fizika nyelvére továbbítjuk, akkor tudasd meg a test útját minden egyes pillanatban. Hogyan határozható meg a sebesség bármely ponton?
Az iskola tanítja, hogyan kell felhívni a kör érintkezését. Az ókori görögök is tudták, hogyan találják meg az érintőket egy ellipszis, egy hiperbola és egy parabolának. Az első általános módszert a probléma megoldására az Archimedes találta. Ez a módszer később a differenciál kalkulus alapjává vált.
Az archimedeai módszer sémája a π szám kiszámításához:
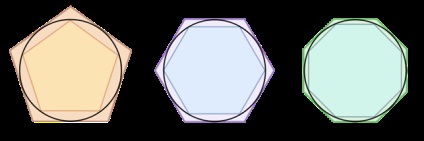
A kerület és az Archimedes által kiszámított átmérő aránya nagyon fontos volt a matematika fejlődéséhez. A körmérésről szóló munkájában Archimedes híres megközelítést adott a π számra: "Archimedean number" 3. Sőt, képes volt megbecsülni a közelítés pontosságát: 3 <π <3 . Для доказательства он построил для круга вписанный и описанный 96-угольники и вычислил длины их сторон.
A matematikában, a fizikában és a csillagászatban nagyon fontos, hogy megtalálja a változó mennyiségek legnagyobb és legkisebb értékét - szélsőségüket. Például, hogyan lehet a labdába írt palackok között megtalálni a legnagyobb volumenű hengert? Mindezeket a problémákat most meg lehet oldani differenciális kalkulus segítségével. Archimédész volt az első, aki látta a kapcsolatot ezekkel a problémákkal és a tangensek meghatározásával kapcsolatos problémákkal, és megmutatta, hogyan oldja meg a szélsőséges problémák.
Ötletek Archimedes közel két évezred előtt az idejüket. Csak a XVII. Században tudósok tudták folytatni és fejleszteni a nagy görög matematikus munkáit.