A matematika leckéje ez a csodálatos kör!
Cél. rendszerezi, általánosítja a diákok tudását; Ismertesse a kör területének kiszámítására szolgáló képleteket, a kör hosszát; képes formában használni a nem szabványos problémák kiszámításához és megoldásához; rajzeszközök használata; hogy szereti a geometriát, kreatív hozzáállást alakítson ki az ügyben; hogy gazdagítsa a történeti tudást a geometria területén.
Berendezés: írásvetítő, különböző átmérőjű színes bögrék, történeti festmények, kiadványok.
Lecke terv:- Szervezési pillanat.
- Felmelegedés: a) Blitz-szavazás; b) képletek, rajzokkal együtt; c) kodoszkóppal (teszttel) dolgozni.
- Problémák megoldása.
- Gyakorlati munka.
- Kerület az építészetben és a népművészetben.
- A történelem ...
- A lecke eredménye.
- Házi feladat.
(A kártyák mögött található táblák rejtett szavak, maguk a kártyákon ezeket a szavakat betűk zűrzavara titkosítja.)
Tanár: srácok! Találd ki a titkos szavakat.
Tanár. Ma a téma: "Ez a csodálatos kör!". Ez a kör. Az ívelt vonalak között ez a legcsodálatosabb. A kör egy zárt vonal. Az általa határolt sík része egy jól ismert kör.
A lecke célja, hogy megismételjük a körkörös terület kiszámításának képletét, a kör hosszát; Alkalmazzon képleteket különböző nem szabványos problémák megoldására, és derítse ki, mi olyan csodálatos a körben.
Tanár: Legyünk felmelegedve. Elkezdem a javaslatokat, és feladata befejezni őket.- A kör középpontjától bármely pontig terjedő távolságot ... (sugarúnak) nevezik.
- A téglalap területét a ... (S = a * b) képlet segítségével számítjuk ki.
- Egy három dimenziójú alakot: a szélességet, a hosszúságot és a magasságot .... (parallelepiped).
- Az R 2, ... képlet alapján számítjuk ki a kör területét.
- Mi a szám neve, megközelítőleg 3,14 ... ("pi" szám).
- Mi számít a 2 ** R .... képlet alapján? (Körülbelül).
- A számok tulajdonságait vizsgáló tudomány neve ... (geometria).
- Mennyi ideig tart, ha a percmutató teljes kört tesz (1 óra).
(A mágneses táblán a tanuló formulákat alkot a kör területének, a kör hosszának, az átmérőnek a sugáron való megtalálásához.) A tanár ebben az időben dolgozik az osztályban.)
Tanár: srácok, gondosan nézzétek meg a rajzot és válaszoljak arra, hány kört építettek?
Hogyan készítsük el ezt a számot?
(Diákok válaszai.) Ellenőrizze a képleteket a mágneses táblán.)
Tanár: És most figyelj a képernyőre! Válassza ki a helyes választ, és indokolja azt.
1. A sugarat egy szegmens képviseli: 1) AB; 2) OD; 3) CD.
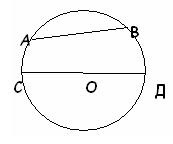
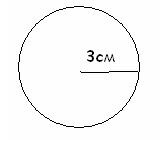
2. Egy adott sugárral rendelkező kör hossza kiszámításra kerül:
2) = 2 ** 3 2 = 18 * (cm); 3) = 2 ** 6 = 12 * (cm).
3. A kör területe 9 * m 2. Mekkora a sugara: 1) R = 9 m, 2) R = 3 m; 3) R = 4,5 m.
Tanár: Jól van, srácok. A bemelegítés vége. A gyakorlatban leírjuk a lecke számát és témáját.
(A bizottság feljegyzi a feladatokat.)
Task number 1. A cár Bell bázisának átmérője 6,6 m. Keresse meg a cárharang bázisterületét, a P számot egészére kerekítik.
A megoldás. R = D: 2, R = 3,3 (m), 3,143, S = * R2 S = 3 * 3,3 2 = 32,67 (m 2).
Válasz. a cárka bázisa 32,67 m 2.
2. feladat. Egy kör alakú furatot fúrnak egy négyszögletes lemezen. Keresse meg a rész területét és tömegét, ha 1 cm 2 súlya 2 g (3. szám).
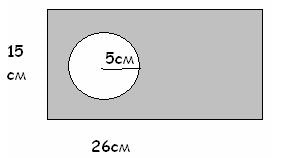
A megoldás. Sokruzhn. = * R 2. Közvetlenül. = a * b, S számok = S egyenes - S-kör, S-ív. = 75 cm 2. Közvetlenül = 390 cm 2. S = 315 cm 2. M = 315 * 2 = 630 (g).
Válasz: a rész területe 315 cm2. A rész tömege 630 g.
Tanár: Srácok, vannak táblázatok az asztalokon. Vegye a színes köröket. Hajlítással keresse meg a központot. Jelölje meg, rajzolja meg a sugarat. Számítsa ki a kör (3) területét.
(A srácok függetlenül dolgoznak, majd a teszt végrehajtásra kerül.) A döntést a táblán rögzítik.)
Független munka (piros kör, R = 2 cm, sárga - 3 cm, zöld - 4 cm, kék - 5 cm).
Tanár: A következő feladat. Kör alakítsa ki és számítsa ki a hosszát. Én egy változat, a sugara 3 cm, a második változat, a sugara 5 cm.
(A srácok függetlenül dolgoznak).
Tanár. Ha helyesen számolsz ki, akkor ha a kifejezést ezzel a kifejezéssel helyettesíted, akkor megfelelő egyenlőséget kapsz. Ellenőrizze (a fedélzeten írott ellenőrzést)
I opció: + 1,16 = 20
II opció: + 68, 6 = 100
Tanár: A kör egy nagyon harmonikus alak. Nem indokolatlan, hogy nemcsak tudósok, matematikusok, hanem építészek, szobrászok, művészek is annyira figyeltek rá. Nézd meg ezeket a reprodukciókat (a tanár saját belátása szerint választhat ilyen reprodukciókat). Ezek a remekművek a kör elemeit látják. A kört a népművészetben találta meg, különösen - faragás. A dísz a körökből és elemeiből áll. (1. ábra), (2. ábra), (3. ábra), (4. ábra).
Tanár: A görbe vonalak legegyszerűbb és ugyanakkor fenséges vonása a kör. Ez az egyik legrégebbi geometriai alak. A babiloniak és az ősi indiánok úgy tekintették a sugarat, mint a kerület legfontosabb elemét. A szó latin és jelentése "sugár". A sugár kifejezést először a Ramus francia tudós "Geometria" című könyvében találja meg, amelyet 1569-ben, majd Francois Vieta-ban publikáltak. A kerület mértéke az átmérőhöz viszonyítva, azaz a P szám, az évszázadok emberiségének legjobb elméjével számolt. "Pi" a görög "perimetron" szó kezdeti betűje, ami azt jelenti, hogy a kör. A P szigorú elméleti megfontolások alapján végzett első számítását az ókori legnagyobb matematikus, Archimedes végezte el, ezt bizonyította. Ötletek Archimedes közel két évezred előtt az idejüket. Csak a XVII. Században tudósok tudták folytatni és fejleszteni a nagy görög matematikus munkáit. Archimedes élt (Kr. E. 287-212 körül) a város Siracusa körül kb. Szicíliában. Egy római harcos kezében halt meg. A halál elıtt Arhimédész azt mondta a katonának: "Ne érintse meg a köröket!" Archimedes 75 éves volt. Mennyibe kerülhetne az emberiség számára szükséges felfedezések?
Tanár: Mit gondolsz, milyen csodálatos a kör?
A gyerekek körét széles körben használják nemcsak a tudományban, hanem a mindennapi életben és a művészetben is.
Tanár: srácok, írja le a házi feladatot. Számítsd ki az öt rubel érme területét.