A logikai függvények minimalizálása
A Boole-függvény minimálisra csökkentésének problémája az, hogy megtaláljuk az egyenértékű képletet, amelynek minimális összetettsége van. A képlet összetettsége alatt értjük a betáplálandó betűk számát. A DNF-ben bemutatott epe funkciók minimalizálására szolgáló módszerek a legfejlettebbek. Ezek a módszerek az egyszerű implikánsok fogalmán alapulnak.
Ha valamilyen logikai függvény # 966; egyenlő nullával ugyanazon a készleten, amelyen egy másik F funkció eltűnik, és néhány más készleten is, akkor azt mondjuk, hogy ez a függvény # 966; belép az F függvénybe, és ez a következménye. A belépési feltétel a következőképpen íródott: jÌF. Például vegye figyelembe az F = X függvénytÅY. Következtetései funkciók
Prime implicants egy Boole F függvény olyan elemi kötőszavak, melyek maguk is részben ez a funkció, de sem saját részét ezek a kötőszavak F nem része a funkciót. Védett rész egy olyan munka, amelyet egy adott munka egy vagy több tényezőjének kizárásával nyerhet. Például egy műnek saját részei vannak:
Például a So számára, és egyszerű függvények a függvény F.
Az egyszerű befoglaló a legrövidebb elemi konjunktúra, amely belép a Boole-függvénybe.
Boole-függvény bármely egyszerű implikáns diszjunkciója. Az összes egyszerű implikátor diszjunkcióját a Boole-függvény csökkentett DNF-jének nevezzük. Számos algoritmus létezik egy csökkentett DNF logikai függvény megszerzésére. Az egyik legfejlettebb a Quine módszer.
Quine módszere. Ez a módszer a CDNF transzformációján alapul a nem tökéletes ragasztással és abszorpcióval.
A ragasztás (teljes) működését a reláció határozza meg
Azt mondják, hogy az XY két tagját össze kell ragasztani az Y változóba.
A tökéletlen ragasztás működését a képlet határozza meg
A jobb oldali oldalon, az eredményül kapott ragasztás X. kifejezésén kívül, a beillesztésben résztvevő mindkét feltétel meg van írva.
Az abszorpció működését a reláció határozza meg
Quine tétele. Ha a Boole-függvény CDNF-ben minden hiányos beillesztési műveletet végzünk, majd az összes abszorpció műveletet, akkor e funkció rövidített DNF-jét kapjuk meg, azaz. diszjunkciója minden egyszerű implikátorának.
Gyakorlatilag rövidítve a DNF alkalmas ilyen szekvenciában.
Végezze el a CDNF-ben az alkotóegység nem teljes beillesztésének lehetséges műveleteit és minden lehetséges abszorpciós műveletet.
Ezután hajtson végre minden lehetséges műveletet a tagok tökéletlen ragasztásával és felszívásával (n -1) betűvel.
Végezzen el minden lehetséges műveletet a tagok tökéletlen ragasztására és felszívására több betűvel (n -2), stb.
A nem tökéletes ragasztás és felszívódás minden lehetséges műveletét négy betűs kötőanyaggal végezzük. Az eredmény a táblázatba kerül:
Ragasztott eredmény száma
Megjegyezzük a rövidített képletet, amely magában foglalja a ragasztás eredményeként létrejött kötőszavakat és az egység azon összetevőit, amelyek nem ragadtak össze:
A kapott kifejezésben ismét elvégezzük a ragasztás és felszívódás minden lehetséges műveletét:
Az első és a negyedik, a második és a harmadik tagot párban összeillesztettük. Az ötödik és hatodik tag marad. Így kapunk:
Ebben a kifejezésben nincsenek olyan kifejezések, amelyek összeilleszkednek, tehát rövidített diszjunktív normális forma. A minimális diszjunktív forma megtalálásához implicit mátrixot használhatunk. Oszlopokban jelölt implikantnoy mátrix komponensek megadott funkcionális egységek, és a vonalak - implicants eredményeként kapott adhéziós (5. táblázat).
Ha implicant valódi részhalmaza az alkotórészek egy elemi cella a mátrix megfelelő e készülék implicants és összetevői, van jelölve egy kereszt. Ahhoz, hogy a minimális diszjunktív normál forma előre meghatározott funkció, hogy megtalálja a minimális számú implicants, amelyek együttesen az összes keresztezéséből implikantnoy oszlopon mátrix. A példában egy adott függvény minimális diszjunktív formája van
.
Előfordulhat, hogy a funkciónak több különböző, ugyanolyan bonyolult formája van.
Carnot (Veitch) térképek. A Carnot térkép egy téglalap, amelyet cellákra osztanak, amelyek száma egyenlő az adott logikai függvény független változóinak összes készletével. Két változó függvényében a térkép négy cellát tartalmaz, 3 változó, 8 cellaként stb. Függvényében.
Tekintsünk egy térképet két változóra (21. ábra). Minden egyes kártyatulcs az egység alkotórészének felel meg.
Ábra. 21. A Carnot térkép a 2. ábrához. 22. Carnot térképe a
3 változó függvényének két változó funkciója
Egy változó hozzáadásával a kártya megduplázódik. Az 1. ábrán. A 22. ábra a Carnot térképet mutatja 3 változó függvényében.
Építésekor a térképet, akkor a következő szabályt: Karnaugh térkép az n-változós függvény nyerik a térképen a funkció n -1 változók, ha ez utóbbi megkétszereződik hozzátéve, hogy ez pontosan ugyanolyan van szimmetrikusan a hosszú él. Ebben az esetben az új kártya felét egy új betű jelöli az igenlő formában, a másik fele pedig azonos betűvel, de negatív. Az 1. ábrán. A 23. ábra a Carnot térképet mutatja a 4 változó függvényében, amely a 2. ábrán látható térképből származik. 22. Egy megfelelően megjelölt térképen két szomszédos cellának felel meg
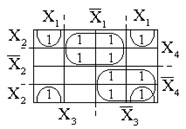
az egység ragasztott összetevői. Ezenkívül a térkép szélein balra és jobbra, vagy tetejére és aljára szimmetrikusan elhelyezkedő bármelyik két cellának is meg kell felelnie az egység összetartó elemeinek.
Egy adott logikai függvény minimalizálása Carnot-kártyával történik ebben a sorrendben.
1. A megadott funkció CDNF-re konvertálódik.
2. Az adott funkció minden egyes egységét a Carnot térkép megfelelő cellájában lévő egységgel jelöljük.
3. Az egymás mellett elhelyezkedő vagy szimmetrikusan a térkép szélein lévő egységek rendszeres négyszögekkel vannak ellátva. A következő követelmények teljesülnek:
- Az egy téglalap alá tartozó egységek száma 2 k. ahol k értéke egész szám;
- Minden téglalapnak minél több egységnek kell lennie, és a téglalapok számának a lehető legkisebbnek kell lennie;
- Egy és ugyanazon egység többször is lefedhető különböző téglalapokkal.
4. Minden téglalap borítású egység esetében olyan összefüggést írunk be, amelybe a négyszög által lefedett egységekhez tartozó betűk belépnek.
5. Írja le a minimális DNF-et. amelyben az összes lefedő téglalapnak megfelelő kötődnek be kell lépniük. Ha a térképen olyan egységek vannak, amelyek el vannak választva a többiektől és nem tartoznak semmilyen téglalapba, akkor az egység megfelelő alkotóelemei hozzá vannak adva a létrejövő diszjunkcióhoz.
6. Ha lehetséges, lerövidítjük az eredményül kapott képletet az általános kifejezések zárójelbe helyezésével.
Egy példa. Vegyünk négy változó funkcióját. Tegyük fel, hogy egy adott függvény SDNF formája:
A csökkentett függvény minden alkotóegységét a Carnot térkép megfelelő cellájában lévő egység jelöli (lásd 23. ábra). Az egyértelműség kedvéért az egységeket borító négyszögeket ovális vonalak jelzik. Ennek a funkciónak a minimális DNF értéke:
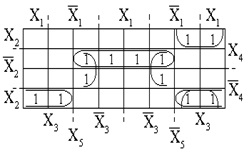
A Carnot térkép öt változó függvényében a 3. ábrán látható. 24. A 6. ábrán látható ¾ változó függvényében. 25. Az öt és hat változó funkciójú Carnot térképek a következő jellemzőkkel rendelkeznek. A kötésösszehúzódások megegyeznek a térképen belül elhelyezkedő egységekkel a szimmetria középső tengelyeihez képest szimmetrikusan.
Egy példa. Hagyja az öt változó függvényét a Carnot térképen feltüntetett egységekkel az ábrán. 24. A bevonat következtében a következő minimális DNF-t kapjuk:
A hat változó funkciójának minimálisra csökkentését a 6. ábrán a térképen lévő egységekkel jelölt függvény segítségével alkalmazzuk. 25. A bevonat következtében:
A Carnot térképen lévő egységek lefedéséből származó következtetések kinyomtatásakor az alábbi függőségek használhatók az ellenőrzéshez: l = n-k. m = 2 k. ahol l a lefedettség következtében kapott betűk száma, m az e téglalap által lefedett egységek száma, k a ragasztás eredményeként elnyelt betűk száma, és n a függvény független változóinak száma.
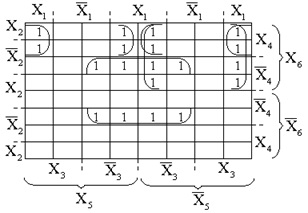
Ábra. 25. Carnot térkép 6 változó függvényében