A logikai függvények minimalizálása - matematika
5. A logikai függvények minimalizálása
Az implicit függvény egy bizonyos logikai függvény, amely eltűnik ugyanazon a változó-készleten, amelyen a funkció maga nulla.
Bármely konjunktív távú (elemi együtt), vagy egy csoport kifejezések, diszjunkció csatlakoztatva karakter tartalmazza PDNF vannak implicants eredeti funkciója
Az elemi összekapcsolódás (kötődési kifejezés), amelyben egy vagy több elsődleges kifejezést távolítanak el, egyszerű implikánsnak nevezik.
Van néhány módszer a logikai funkciók minimalizálására jelenleg. Mindegyikük általában két szakaszból áll. Az első lépés az, hogy megkapjuk az összes egyszerű implikátor listáját, azaz rövidített DNP. A második szakaszban, a bevonatok táblázatát használva, távolítsuk el az "extra" fogalmakat, amelyeket más implikánsok fedeznek. Ennek eredményeként olyan DNF-t kapunk, amelyből nem lehet eltávolítani a befoglaló anyagokat. Az ilyen DNF-t holtpontnak hívják.
5.1 A Quine módszer
Az első szakaszban a módszer Quine párok össze minden implicants szereplő PDNF, annak érdekében, hogy azonosítsa a lehetőségét, felszívódását néhány változó alapján a törvény a ragasztás:
.
Az eljárás addig folytatódik, amíg egy tag nem marad, ami lehetővé teszi a felszívódást egy másik kifejezéssel. Ennek eredményeképpen számos egyszerű implikátort kapunk. Ezeknek az implikánsoknak a diszjunkciója rövidített DNP.
A második szakaszban egy burkolási táblát készítünk, a táblázat sorai pedig a feltüntetett egyszerű implikánsokat és az oszlopokban - az eredeti funkciókifejezés kifejezéseit. A táblázatos sejtek akkor jelennek meg, ha egyszerű kifejezést tartalmaz egy kifejezésre. Ennek eredményeként a Boole-függvény minimalizálása csökkenti az ilyen oszlopokat lefedő minimális számú egyszerű implikáns szám megtalálását. Ennek eredményeképpen egy zsákutcából származó DNF-t kapunk.
A módszer hátránya, hogy az első szakaszban minden konjunktikus kifejezés párhuzamos összehasonlításra van szükség, amikor egyszerű implikánsokat találunk. A kezdeti kifejezések számának növekedésével párhuzamosan növekszik a páronkénti összehasonlítások száma, ami bonyolítja a minimalizációs probléma megoldását.
5.2 A Quine módszer n-dimenziós kockák használatával
Ez a módszer kiküszöböli az előző módszer hátrányát, azaz Ez szükségtelenné teszi a páros összehasonlítások valamennyi kifejezés az első lépés megtalálása az elsődleges implicants. Ahhoz, hogy ezt elérjük, megépíteni az n-dimenziós kocka, amely akkor vizuálisan azonosítani konjunktív távú kötés, amelyek generálják egyszerű implicants.
A Boole-függvény minimalizálására vonatkozó probléma megoldásakor a konjunktív kifejezések helyett kényelmes bináris készleteket használnak.
Minimálisra csökkentse a Boole-függvényt
.
A zárójelben a megfelelő bináris halmazok decimális ekvivalensei vannak.
A funkciót CDNF formában reprezentáljuk:
A konjunktív kifejezéseket bináris halmazok formájában írjuk:
.
Construct egység 4 - dimenziós kocka, és válasszuk csúcsok megfelelő bináris készletek szerepel a megadott Boole-függvény (10. ábra):
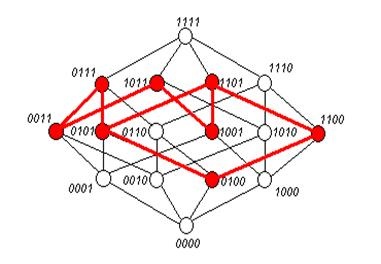
1 szakasz. A rövidített DNP meghatározása.
A ragasztási törvényt alkalmazzuk egy kocka csúcspontjainak (bináris készletekre), amelyek egy élre kapcsolódnak:
A kötőjel azt jelzi, hogy ebben a helyen nincs változó.
Néhány egyszerű fogalmazó esetében a ragasztás folytatható:
Az idempotencia törvénye szerint:
Az eredményül kapott egyszerű implikáns diszjunkció rövidített DNP:
2 szakasz. A zsákutcának a meghatározása DNF.
A zsákutcából álló DNF meghatározásához egy burkolólapot kell összeállítanunk, amely tartalmazhat olyan bináris készleteket, amelyek nem vettek részt a ragasztásban:
A táblázat összes oszlopát lefedő sorok minimális számának meghatározásával megtaláljuk a holtpontot DNF:
A módszer hátránya az, hogy egy n-dimenziós kockát építenek, mert számos változó esetében ez az építkezés nehéz.
5.3 A Quine-McCluskey módszer
A Quine-McCluskey módszer az előző módszer, de n-dimenziós kockák geometriai felépítése nélkül: a kockák jelen vannak, de absztraktek.
A módszer a DNF konjunktív kifejezéseinek köbös ábrázolásán alapul, ahol a kockák eloszlása az azonos számú csoportba tartozó alcsoportokba történik. A particionálás lehetővé teszi az egyes csoportok kockáinak összehasonlítását, amelyek szomszédosak az egységek számában, a keresések számának csökkentése érdekében.
Az iteratív minimalizálási eljárásban párhuzamos összehasonlítást lehet végezni csak a szomszédos csoportok között.
Egyszerű beavatkozás az első szakaszra:
1. Minden kezdeti konjunktikus kifejezést bináris készleteik formájában írnak.
2. Az összes készletet diszjunktív csoportokra osztják. Az r-kocka kialakulásának feltétele az (r-1) -cube-ek közötti eltérés, csak egyetlen koordinátával, egy bináris számjeggyel és közös független koordináták jelenlétével.
3. Az i-csoport tartalmazza az összes olyan bináris készletet, melynek rekordja i egysége van.
4. Pairwise összehasonlítás csak a szomszédos csoportok száma szerint történik. Olyan csoportok, amelyek két vagy több számmal különböznek egymástól, nincs értelme összehasonlítani.
Minimálisra csökkentse a Boole-függvényt
Információ a "Matematikai logika" munkájáról
Szakasz: Matematika
Karakterkészletek száma: 29947
A táblázatok száma: 14
Képek száma: 9
állítson fel vagy tagadja meg a tárgyak és a valóság jelenségei közötti bármilyen kapcsolatot. 3. Matematikai logika és "józan ész" a 21. században. A logika nemcsak matematikai, hanem filozófiai tudomány. A huszadik században a logika két egymással összekapcsolt hypostázisa különböző irányokban elváltak. Egyrészt a logikát úgy értjük, mint a helyes gondolkodás törvényeit.
szórakoztató. A gyakorlatok ugyanolyan típusúak. Ezért egyszerűen szükséges kiegészíteni a feladatkönyvet az ún. II. Fejezet. Az algebra és a matematikai logika elemeinek vizsgálata. § 1. A numerikus kifejezések, a változókkal kifejezett kifejezések, a numerikus egyenlıtlenségek és egyenlıtlenségek tanulmányozása, egyenletek. A numerikus kifejezések, egyenlõtlenségek és egyenlõtlenségek tanulmányozása, a.
kijelentés "Soha nem használom a matematikai logika módszereit." Nyilvánvalóan ellentmondanak egymásnak, de lehetnek egyidejűleg hamisak is. Például, ha matematikai logika specialistája vagy, akkor gyakran használd a módszereket, de alig van szükséged az életed minden napjára. A kizárt középosztály törvényét az egzakt tudományok területén használják.
feltételezi a D (azaz axiómák Ax # 204; F # 205; A * és deduktív eszközök P # 204; Fn + 1), akkor beszélünk egy elmélet felépítéséről, mint az F.S. =