Grafikusan oldja meg a problémát, lineáris programozást, példákat a problémák megoldására
A feladat. A lineáris programozási probléma grafikus megoldása a célfüggvény szélsőértékének meghatározásával:
Megalkotjuk az elfogadható megoldások területét, azaz Az egyenlőtlenségek rendszerét grafikusan oldjuk meg. Ehhez minden vonalat meg kell alkotnunk, és meg kell határoznunk az egyenlőtlenségek által adott fél-síkot (a fél síkokat elsődleges jelöli).
A két egyenlet 3x1 + x2 = 9 egyenletét állítjuk össze.
Ahhoz, hogy megtalálja az első pontban egyenlővé x1 = 0. Azt találják x2 = 9, hogy megtalálják a második pont egyenlővé x2 = 0. találni x1 = 3 csatlakozik (0, 9) (3, 0) egy egyenes vonal. Meghatározzuk az egyenlőtlenség által adott fél síkot. Kiválasztása egy pontot (0, 0) meghatározza az egyenlőtlenség jele a fele: 3 1 + 0 • • 0-9 ≤ 0, azaz, 3x1 + x2 - 9≥ 0 a vonal fölötti fél síkban.
Az x1 + 2x2 = 8 egyenletet két pontra építjük.
Ahhoz, hogy megtalálja az első pontban egyenlővé x1 = 0. Azt találják x2 = 4. Ahhoz, hogy megtalálja a második pont egyenlővé x2 = 0. találni x1 = 8. csatlakozik (0, 4), (8, 0) egy egyenes vonal. Meghatározzuk az egyenlőtlenség által adott fél síkot. A pont kiválasztása (0; 0) meghatározzuk az egyenlőtlenség jeleit a fél síkban: 1 • 0 + 2 • 0 - 8 ≤ 0, azaz. x1 + 2x2 - 8≥ 0 a félvonalon a vonal felett.
Az x1 + x2 = 8 egyenletet két pontra állítjuk össze.
Ahhoz, hogy megtalálja az első pontban egyenlővé x1 = 0. Azt találják x2 = 8. Ahhoz, hogy megtalálja a második pont egyenlővé x2 = 0. találni x1 = 8. csatlakozik (0, 8) (8, 0) egy egyenes vonal. Meghatározzuk az egyenlőtlenség által adott fél síkot. Kiválasztása egy pontot (0, 0) meghatározza az egyenlőtlenség jele a fél-1 • • 0 + 1 0-8 ≤ 0; x1 + x2 - 8≤ 0 a vonal alatti fél síkban.
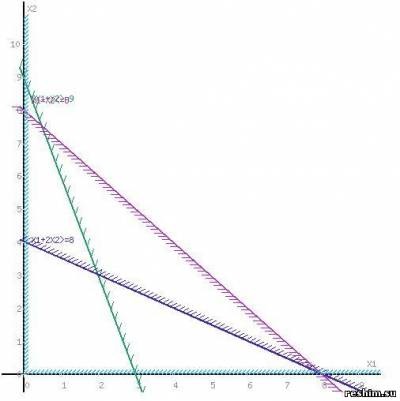
A fél-síkok metszéspontja egy olyan tartomány lesz, amelynek pontok koordinátái megfelelnek annak a feltételnek, hogy a probléma korlátait az egyenlőtlenségek képezik.
Jelöljük a megoldások poligonjának határait.
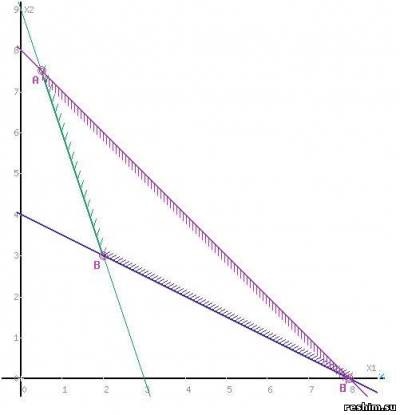
A számológéppel ellenőrizheti a funkciógrafikonok ábrázolásának helyességét
A probléma objektív függvényét F = 4x1 + 6x2 → min.
Construct megfelelő sorban függvény F érték = 0: F = 4x1 + 6x2 = 0. A vektor gradiens az együtthatók a célfüggvény minimalizálása mutatja azt az irányt az F (X). A vektor kezdete a pont (0; 0), a vég a pont (4; 6). Ez a vonal párhuzamosan fog mozogni. Mivel minket érdekel a minimális megoldás, ezért a vonalat a kijelölt régió első érintéséig mozgatjuk. A grafikonon ezt a sort egy szaggatott vonal jelzi.
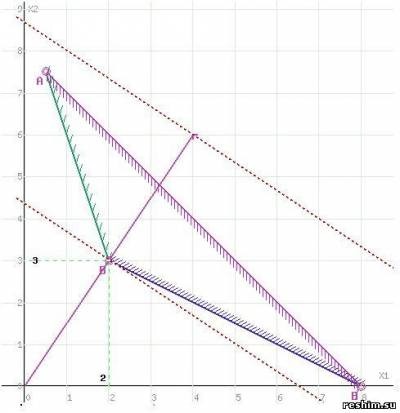
Az F (x) = 4x1 + 6x2 egyenes metszi a régiót a B ponton. Mivel a B pontot az (1) és (2) vonalak metszéséből származtatjuk. akkor a koordinátái megfelelnek e sorok egyenleteinek:
3x1 + x2 = 9
x1 + 2x2 = 8
Az egyenletek rendszerének megoldása: x1 = 2, x2 = 3
Honnan találjuk az objektumfunkció minimális értékét:
F (X) = 4 * 2 + 6 * 3 = 26