A négyszög területe
A világgeometria kialakításának legősibb koncepciói a sok egyenes vonalú területek, köztük: téglalap, paralelogramma, háromszög és trapéz alakú területek fogalmai. Még a 7. században a téglalap alakú négyzet kiszámította az egyiptomiakat. Szélesítették a hosszúságot.
A babilóniai aritmetika és az algebra is eléggé fejlett volt, amint azt az ásatások során talált ékszernövényes tabletták is bizonyítják. A babiloni geometriának volt egy elgondolása a párhuzamos vonalakkal, valamint a pitagorai tétellel szegmentált szegmensek arányosságával, sőt egyes számok mennyiségének és területeinek kiszámolásával. Ugyanakkor a babiloniak konkrét objektumokat vettek fel a mindennapi életből a térbeli alakok alatt. Például a körkörös épületek kialakításakor a három átmérő kerületének körvonalait körülírták. A téglalap területét az elvégzett lépések száma alapján számítottuk ki. Nyilvánvalóan ez idő alatt a jelentések ilyen definíciói meglehetősen elfogadhatóak voltak. Ez az alkalmazott geometria a világ sok népére jellemző volt, és széles körben használták a különböző vitatható hazai kérdések megoldását.
Az ő idejének kiemelkedő tudósa, Archimédé, aki számjegyek négyzetét bizonyítja, a kimerültség módszerét alkalmazta. Valójában ez nem más, mint közvetett bizonyíték, amely az ellenkezőjétől indul. Archimédész módszerének fő ötlete az, hogy az ábrán belül, amelynek területét keresik, meg kell adni a megfelelő számokat. A kimerültség módszereinek felhasználásával kiemelkedő tudós számos tétel bizonyítására képes.
Tétel: a négyszög területe megegyezik a szomszédos oldalak termékeivel.
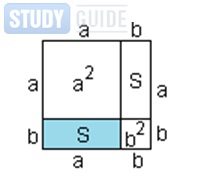
Fordítsa négyszögünket négyzetünkre. Ehhez növeljük oldalának b oldalhosszát a
Ennek eredményeként négy négyzetet kaptunk. Tudjuk, hogy a négyzet a (a + b) 2. Ugyanakkor ezek a négyzetek két téglalapból állnak: egy téglalap, S területével és ugyanazon téglalappal, ugyanazon a területen, valamint két négyzet a 2 és b 2 területekkel. Attól a ténytől függően, hogy a négyszögünk nem egy négyszögből áll, hanem többből is, annak területe megegyezik e négyszögek összes területének összegével. Ez a négyzetek tulajdonából származik:
(A + b) 2 = S + S + 2 + b, vagy 2. egy 2 + 2ab + b 2 = 2S + a 2 + b 2.
Ez azt jelenti, hogy S = ab. Ez azt jelenti, hogy a tételünk bizonyított.