Permutációk, kombinatorikus anyagok, problémák megoldási példái
Az n sorrendű permutációja egy véges n elemelem bijektív leképezése önmagába.
&space;1&space;&space;2&space;3&space;4 # 92; # 92;&space;2&space;&space;413&space;# 92; end "/>, ami egy permutációt jelent,Szintén átrendezheti az oszlopokat a kényelem érdekében:
Az egyértelműség érdekében ugyanaz a permutáció ábrázolható az űrlap képével
Példa a permutációk termékeinek kiszámítására. ha
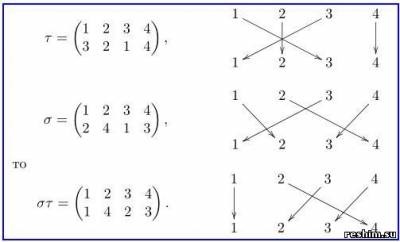
Segítségével a szokásos definíció kényelmes számítani a terméket az alábbiak szerint: a permutációs σ átrendezni az oszlopok úgy, hogy az első sorban a σ egybeesik az utolsó sort a τ. Ezután a termék permutáció, amelynek első vonala standard, a második pedig a σ második sor.
2. példa. Megtalálhatjuk a permutációkat és így tovább
Az első permutáció egyből kettőt, a második kettőt pedig hétbe fordítja, így a munka hétre, és így tovább.
Az átfolyók kényelmesen megszorozzák abban az esetben, ha azokat a diszjunkt ciklusok termékének tekintik.
Például: στ = (1,2,4,3) · (1,3) = (2,4,3)
Így a termék így kiderül: minden 1-től 4-ig terjedő elemhez át kell adni a bal oldali ciklusokat, és nyomon kell követni, hogy hol halad.
Különösen a 3 először 1 (ciklus (1,3)),
majd 1 2-ben (ciklus (1 2. 2. 4. 3)).
Ezért a 3 termék átkerül a 2-re.
A permutációk szorzása nem kommutatív: τσ ≠ στ.
Így a forma egyenleteinek megoldása: τx = σ, xτ = σ
x = τ -1 σ, x = στ -1