Leíró geometria 1
AZ OROSZ FEDERÁCIÓ OKTATÁSI ÉS TUDOMÁNYOS MINISZTÉRIUMA
SZOCIÁLIS KÖZGYŰLÉSI OKTATÁSI INTÉZMÉNY
NEMZETKÖZI SZAKKÉPZÉS "Nizhny Novgorod Állami Műszaki Egyetem. RE ALEXEEVA »
IY Skobeleva, I.A. Shirshov
Ajánlott a Tudományos Tanács a Nizhny Novgorod Állami Műszaki Egyetem. RE Alekseeva tankönyvként a távoktatás és a távoktatás hallgatói számára
technikai specialitások képzésének formái
UDC 514.18 BBK 22.151.1
egyetemi docens, műszaki tudomány kandidátusa, vezető. A leírórajz és grafika elnöke, VGAVT
Skobeleva I.Yu. Shirshova I.A.
A "Leíró geometria" kurzus anyagai kerülnek bemutatásra. Megfontolják a térbeli tárgyak építésének módszereit, pozíciós és metrikus problémákat mutatnak be, amelyek kizárólag gyakorlati jelentőséggel bírnak. Példák a tipikus feladatok megoldására, a független hallgatói megoldásokra, a grafikai munkákra vonatkozó megoldások és változatok példáira.
A módszeres juttatást a levelező és a távoktatási formák hallgatói használhatják.
Műszaki szakirányú hallgatók számára készült.
Ábra. 230. táblázat. 8. Bibliograf. 11 név.
UDC 514.18 BBK 22.151.1
F egy geometriai alak;
A. B. C. C. D. E. E. G. G. H. I. I. J. K. L. M. N. O. P. Q. R. S. S. T. U. V. W. X. X. Y. Z-pontok az űrben (a latin betű nagybetűi);
a. b. c. d. e. f. g. h. i. j. k. l. m. n. o. o. q. r. s. t. u. v. w. x. y. z-egyenes és ívelt vonalak a térben (kisbetűk a latin ábécé);
Αα (Alfa), Ββ (Beta), Γγ (Gamma), Δδ (Delta), Εε (Epsilon) Ζζ (zéta), Ηη (Ez), Θθ (Theta), Ιι (Iota) Κκ (kappa) Λλ (Lambda), Μμ (MU), Νν (Ny), Ξξ (Xi), Οο (Omicron), Ππ (Pi), Ρρ (Po), Σσς (Sigma), Ττ (Tau), Υυ (Epsilon) ff (Phi), xx (Hee), Ψψ (Psi), Ωω (Omega) - sík és szögek (a betűk a görög ábécé).
(AB) az A és B pontokon áthaladó, határtalan hossza; [AB] - az A. ponthoz tartozó sugár, a B ponton áthaladva;
[AB] az A és B pontok által határolt vonalszakasz; | | AB | - az A ponttól a B. pontig tartó távolság;
| | A, a | - az A ponttól az egyenes a vonalig; | | A, α | távolság az A ponttól az α síkig.
A geometriai képek közötti kapcsolatot kifejező jelek:
= - egyenlőség, egybeesés, - leképezés, - így;
- ha (csak abban az esetben), egyenértékűség;
× - metszéspont abban az esetben, ha a keresztezési eredmény az A = c × d pont;
- metszéspont abban az esetben, ha a keresztezés eredménye a pontok halmaza: a = × γ;
- tartozék: A α; - felvétel: A α;
- csatlakozni: ABC = [AB] [BC] [CA];
"A tudományt kísérő varázslat legyőzheti az emberek elme iránti elkeseredettségét az emberek különös feszültségéért, és örömet okoz az elmének gyakorlása során -, hogy a legtöbb ember fárasztónak és unalmasnak tűnik"
A leíró geometria elmélete a mérnöki gyakorlat, geometriai és mérnöki előkészítés alapja.
A kézikönyv megépítésére szolgáló eljárásra műszaki rajz és széles körben használt, a vizuális megjelenítés: kifejező vetítőobjektívet és hangerő modeli.Geometricheskie problémákat megoldani, ugyanakkor a komplex rajzok és vizuális képeket egy és ugyanazon szabályok. Mint látható a tapasztalat, a használata a vizuális megjelenítés megkönnyíti céltudatos kialakulását téri reprezentációk és a fejlesztés a térbeli képzelőerő, az olvasás-tanulási rajzok, geometriai tervezés.
Jegyzet optimálisan megszervezni önálló hallgatói munka, mivel ez tartalmazza az elméleti alapok a természetesen a leírás által kibocsátott hallgatók grafikai munka ábrázoló geometria ajánlásokat azok végrehajtásának bemutatását, megoldások és fokozatos végrehajtás rajzok induló eljárás rajzok munkát a megvalósítások és példák ilyen művek.
1. A TANULMÁNY TÁRGYA
1.1. Leíró geometriai módszer
1.2. Leíró geometriai problémák
A leíró geometria két fő kérdéssel foglalkozik:
1. A síkban lévő háromdimenziós térbeli formák képalkotásának módszereinek vizsgálata.
2. Térbeli formák tanulmányozása lapos képektől. A rajzok alapvető követelményei:
a végrehajtás egyszerűsége és pontossága,
reverzibilitást, vagyis annak a lehetőségét, hogy megoldja a bemutatott tárgy alakjának és méretének visszaállítását.
2. A PROJEKCIÓS MÓDSZEREK
2.1. Központi vetítési módszer
A térben válasszon ki egy tetszőleges S pontot a vetületi középpontnak és a II síknak - a vetületek síkját vagy a képsíkot (2.1. Ábra). Egy objektum központi vetületének megszerzéséhez, például egy AB szegmenshez. szükséges
a vetületek középpontján és a tárgy minden pontján (A és B pont), hogy egyenes vonalakat húzzon a képsík kereszteződéséhez. Ezeket a vonalakat sugárzásnak nevezzük. A vetületi sugár keresztezési pontját a képsíkjával a pont vetítésével nevezzük a síkra.
Egy objektum egy síkra történő vetülete az adott síkra mutató összes pontjának vetületeinek halmaza.
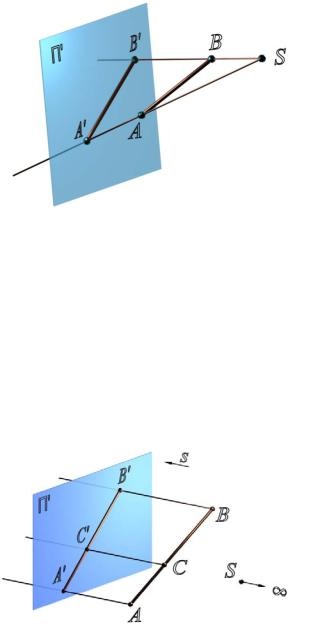
Ábra. 2.1. Központi vetítési módszer:
[SA] és [SB] - vetítőgerendák;
Az SA П és B SB П az A síkban lévő A és B pontok középpontja
A központi vetítési eljárással kapott rajzok nagyon világosak, mivel ugyanolyan elven alapulnak, mint az emberi látómező. Az ilyen rajzokat azonban nehéz elvégezni és mérni, mert az objektum mérete torzult.
2.2. Párhuzamos metszési módszer
Ha a vetületek középpontja a végtelenbe kerül, akkor a sugárzások közötti szög nulla, és a sugárzási sugarak párhuzamosak (2.2. Ábra).
Ábra. 2.2. Párhuzamos vetítési módszer: s - vetítési irány;
[SA], [SB] és [SC] - vetítőgerendák;
A. B és C az A, B és C pontok párhuzamos vetületei az Π síkra s irányba
2.3. A párhuzamos vetületek tulajdonságai
1. A pont kivetítése a lényeg (lásd a 2.2. Ábrát).
2. Az egyenes vonal egyenes vonal (lásd a 2.2. Ábrát), kivéve ha az egyenes vonal párhuzamos a kivetítés irányával.
3. Ha a kivetítőt párhuzamosan vetíti előre, az arányok továbbra is fennmaradnak.
4. Ha a pont egy vonalhoz tartozik, akkor ennek a pontnak a vetülete a C AB C A B vonal vetületéhez tartozik (lásd a 2.2. Ábrát).
5. Ha a vonalak egymással párhuzamosak, a vetületeik párhuzamosak is (1.3. Ábra).
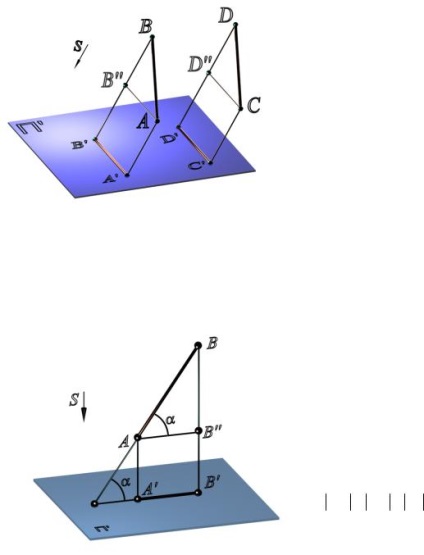
Ábra. 2.3. Párhuzamos vonalak vetületei:
AB // DC; A B // D 'C'
2.4. Ortogonális vetületek
Ha a vetítési irányt s síkra merőleges a vetítés, az előrejelzési módszer az úgynevezett ortogonális (2.4 ábra.), Majd a kapott vetítés - ortogonális.
Ábra. 2.4. Ortográfiai vetület: s P,
Az ortográfiai vetület egy párhuzamos vetület egyedi esete, és ugyanazokkal a tulajdonságokkal rendelkezik.
Az egyik vetítő síkra történő kivágás során kapott képek nem reverzíbilisek, vagyis az eredeti A-projektor eredeti helyreállításának problémája nem megoldható egyedileg. Az AA síkbeli sugáron elhelyezkedő pontok előrejelzései a II síkban egybeesnek.
A reverzibilis rajzok beszerzéséhez néhány további feltételre van szükség. Például, az ábrázolt objektum mereven kapcsolódik a koordináta tengelyéhez és egy velük tervezett síkra. Az ilyen rajzokat axonometrikusnak nevezik. Egy másik módszer az, hogy az objektum több, egymásra merőleges vetületre van vetítve. Az ilyen rajzokat ortogonálisnak nevezik, és a legszélesebb körben használják a mérnöki munkát.