A testmozgás általános esete (a sebességeknél)
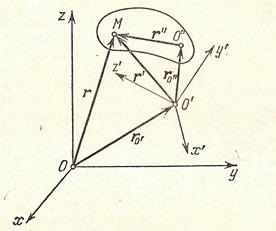
Vegye figyelembe a következő problémát az általános megfogalmazásban. Szilárd végez tetszőleges képest mozgásban a koordináta-rendszer O'x'y'z „(50. ábra), ami viszont mozog önkényesen viszonyítva rögzített koordináta-rendszerben Ohuz. Meg kell határozni egy merev test abszolút mozgását, azaz Mozgás az Oxyz koordinátarendszerrel kapcsolatban. A test mozgása tekintetében a rendszer O'x'y'z „határozza meg a relatív sebessége pólusai O„, és a vektor relatív szögletes SKO-körül erősödik a pillanatnyi forgástengely áthalad a pole O hordozható mozgás, azaz a. E. A mozgatórendszer O” x'y'z „felé Ohuz. kérünk abszolút sebessége pólusú D”, és a vektort a szögsebesség a pillanatnyi átmenő tengely O”. meghatározó abszolút sebessége hazugság-pole„, és az abszolút szögsebessége a test. Egy tetszőleges M pontnak egy olyan test számára, amelynek pozícióját a testben vektor-sugár határozhatja meg. a relatív rendszerben - a vektor-sugárban és végül az abszolút rendszerben - vektor-sugárban. a hozzáadás tétele, van
az első két kifejezés összesítve adja meg az M ponthoz tartozó hordozható sebességet, és az utolsó kettő adja hozzá a relatív sebességét. Megjegyezve, hogy (50
Az első két kifejezés az O "mező átviteli sebességét mutatja, amely ugyanazon pólus relatív sebességével együtt adja meg a pólus abszolút sebességét:
A helyettesítési érték (2,44)
Másrészt az abszolút mozgás definíciója szerint az M pont sebessége a következőképpen ábrázolható
Így jutunk a következő terem hozzátéve szilárd mozgások: sebességeloszlás a abszolút mozgás egy merev test határozza megadásával abszolút sebessége a test pólusok egyenlő a geometriai összege a hordozható és a relatív sebességek pólus, és az abszolút szögsebessége a test, egyenlő a geometriai összege a hordozható és relatív szögsebessége egy test.
Kérdések önvizsgálatra a kinematikában.
1. Vektor képlet egy pont sebességét. Mi az a pont sebessége, ha a mozgását törvény adja
2. A pont gyorsulásához használt vektor képlet. Mi a pont felgyorsulása, ha mozgását a x (t) =
3. A pont normál gyorsulásának képletét. Mikor van nulla?
4. Mi a pont tangenciális gyorsulása, ha mozgását törvény írja elő?
5. Hogyan irányul a szögsebesség vektora és a test szögsebészeti vektora a rögzített tengely körül?
6. Milyen gyorsasága van a testnek a rögzített tengely körüli forgatásával kapcsolatban?
7. Mi az egyenlő és hogyan van az ostreme gyorsulás iránya (skaláris és vektoros felvétel)?
8. A síkkép pontjai sebességének vektoros formulája rajzolja a sebesség tervét.
9. Határozza meg a 3. ábrán látható sík alakú sebesség sebességét és szögsebességét. ha ismert. AB = 1 m, # 945; = π / 4, # 946; = π / 6.
Határozzuk meg az AB és BC rúd szögsebességét, ha az OA rúd szögsebessége van # 969; = 2 (1 / sec), az OAB = 2π / 3 szög, az ABC-egyenes vonal OA = AB = BC / 2.
11. Adjon példákat a pillanatnyi sebességközpont helyére. Hol van a mg. ebben a példában az AB rúd sebességének középpontja?
12. Határozza meg a rúd szögsebességét és szögsebességét. ha AB = l.
13. Milyen szögek határozzák meg a test pozícióját, amely egy rögzített pont körül forog?
14. A vektor formula a test pontjai sebességének meghatározására egy fix pont körül.
16. A sebességek hozzáadására szolgáló vektor formula, mi a pont hordozható sebessége?
17. Vektoros képlet gyorsításhoz.
18. Mi a pont abszolút gyorsulása ebben a példában? Az R sugarú gyűrű egy állandó tengely körül forog, állandó szögsebességgel # 969; Egy állandó sebességű pont u mozog a gyűrű mentén. Határozza meg a pont abszolút gyorsulását, amikor felső helyzetben van.
19. Mi a Coriolis (formula) gyorsítása, amely nulla?
20. Mi az az egyenlőség és az irány a Coriolis gyorsulás egy pont mozgó 2 m / s sebességgel mentén AB összekötő rúd. Ha az OA forgattyú 1 rad / s szögsebességgel forog. A forgattyú vízszintes síkjának szöge π / 3, AB = 3 AO?
21. A test elfordulási sebessége a párhuzamos tengelyekhez viszonyítva. Mi a pillanatnyi előretekerés?
48. Írja Willys képletét.