A folytonos energia sokszorosai
Végtelen sorozatok vannak, amelyek elemeit nem lehet újraszámozni. Az ilyen készleteket megszámlálhatatlannak hívják.
Cantor tétele. A [0, 1] összes pontjának halmaza megszámolhatatlan.
Adjuk meg a [0, 1] pontok sorszámát. Ezért ezek a pontok újraszámozhatók, vagyis x1 sorrendben rendezhetők. x2 ... xn. ....
A [0, 1] intervallumot három egyenlő részre osztjuk. Bárhol az x1 pont található. nem tartozhat minden szegmenshez. . . Ezért köztük van egy D1 szegmens. nem tartalmazza az x1 pontot (1.7. ábra). Ezt a D1 szegmenst vesszük és három egyenlő részre osztjuk. Közöttük mindig van egy D2 szegmens. nem tartalmazza az x2 pontot. Ezt a szegmenst három egyenlő részre osztjuk, és így tovább: D1 szegmensek sorozatát kapjuk É D2 É D3 É...Édn É.... A Cantor axiómájánál az x egy bizonyos pontig konvergál a n ® -ig. Építésképpen ez az x pont mindegyik D1 szegmenshez tartozik. D2. D3, ..., Dn. ..., vagyis nem lehet egybeesni az x1 pont bármelyikével. x2, ... xn. ..., vagyis az x1 sorozatot. x2 ... xn. ... nem üríti ki az összes [0, 1] pontot, ami ellentmond az eredeti feltételezésnek. A tétel bizonyított.
A [0, 1] intervallum összes pontjának halmazához tartozó készletet a folytonosság hatalomcsoportjaként nevezik.
Mivel az intervallumok, a szegmensek és az egész vonal halmazai egyenértékűek egymással, mindegyikük rendelkezik a folytonosság erejével.
Annak bizonyítása érdekében, hogy egy adott készletnek van egy folytonossága, elég egy adott egyezés és egy szegmens, intervallum vagy az egész vonal közötti egyenkénti megfeleltetés jelzése.
Az 1. ábrából. 1.8 ebből következik, hogy az y = x2 parabola pontjai halmaza megegyezik az egyenes pont pontjával - ¥ 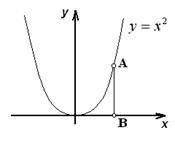
A folytonos teljesítményt a következő tételekkel is meghatározhatjuk a folytonosság kardinalitásának készleteivel (bizonyítás nélkül).
1. tétel. A számlálható készlet összes alcsoportjának sorozata számítható.
Tétel 2. Az irracionális számok halmaza a folytonosság kardinalitásával rendelkezik.
3. tétel. Az n-dimenziós tér minden pontjának halmaza bármelyik n számára a folytonosság kardinalitása.
Tétel 4. A komplex számok halmaza a folytonosság kardinalitásával rendelkezik.
Tétel 5. Az [a. b] a folytonosság kardinalitása.
Így a végtelen készletek ereje különbözhet. A folytonosság hatalma nagyobb, mint a megszámlálható készlet kardinalitása. Az a kérdésre adott válasz, hogy léteznek-e nagyobb folytonosságú halmazok, mint a folytonosság hatalma, a következő tétel (bizonyíték nélkül adható meg).
A magasabb kardinalitási sorozatok tétele. Az adott készlet összes részhalmazának halmaza magasabb, mint egy adott készlet.
Ebből a tételből következik, hogy nincs beállítva maximális kardinalitás.
Témakérdések a témához 1
1. Hagyja a Î A. Következik-e az, hogy a> A?
2. Abban az esetben AA ÇIn?
3. Adja meg azt a készletet, amely bármelyik részhalmaz részhalmaza.
4. A készlet egyenértékű-e a részhalmazával?
5. A készlet ereje nagyobb: a természetes számok vagy a [0, 1] pontok halmaza?