A fa mélysége (Graph Theory)
Gráfelmélet, a mélység a fa egy csatlakoztatott irányítatlan gráf G - egy numerikus invariánsa G. minimum famagasságot Tremaux [en] az supergraphs gráf Ez állandó és hasonló fogalmak találhatók különböző nevek alatt a szakirodalomban, beleértve a több rangsor tetején megrendelt kromatikus száma, a legkisebb magasságot kizárja a fát. A koncepció is közel van az olyan fogalmak, mint a ciklikus pozícióját [en] irányított gráfok és magassága iteráció reguláris nyelvek nyelv [1]. Ösztönösen, ha a szélessége a fagráf azt méri, hogy a grafikon messze van a fa, a fa mélységét méri, hogy a gráf messze a csillag.
A G gráffa mélysége meghatározható az F erdő minimális magasságának olyan tulajdonsággal, amelyet a G gráf bármelyik élének összekapcsolja egy ős-gyermek kapcsolattal összekapcsolt csúcsok F-ben [2]. Ha G kapcsolódik, ez az erdő legyen az egyetlen fa. Az erdőnek nem kell a G. gráf részgrafikája, de ha igen, akkor ez a Tremo fa G.
Az F-ben lévő ős-gyermek párok egy triviálisan tökéletes grafikát alkotnak. és az F magasság a grafikon legnagyobb klikkének a mérete. Így a fa mélysége alternatív módon a legnagyobb gráfméretnek a G. gráf triviálisan tökéletes szupergráfiájában is megadható. Ez a fa szélességének tükrözött képe. amely egy kisebb, mint a G-görbe akkordos szupergráfiájának legnagyobb klikkének nagysága [3]
Egy másik meghatározás a következő:
ahol V a G és G i gráf csúcsainak halmaza G [4] összekapcsolt elemei. Ez a meghatározás tükrözi a [en] orientált grafikonok ciklikus rangját, amely szigorú kapcsolatot és szigorúan összekapcsolt komponenseket használ a nem irányított kapcsolatok és a csatlakoztatott összetevők helyett.
A fa mélysége a grafikonok színezésével határozható meg. A gráf középpontos színezése egy olyan csúcsfestés, amely tulajdonsággal rendelkezik, hogy bármely kapcsolódó generált subgraph esetében egy színes, amely pontosan egyszer fordul elő. Ezután a fa mélysége a grafikon központosított színezéséhez szükséges színek minimális mérete. Ha F egy erdő, amelynek magassága d. rendelkeznek azzal a tulajdonsággal, hogy bármely G gráf szélén csatlakozik ős és leszármazott fa, akkor lehetséges színező a gráf Gd központú virágok színezés minden csúcs színű, számos, egyenlő azzal a távolsággal a gyökér a grafikon F [5].
Végül fiktív játékként definiálhatod. Pontosabban, csakúgy, mint a "rendőri rablók" játék. A következő játékot egy irányítatlan grafikonon képviseljük. Két játékos van, rabló és rendőr. A rablónak van egy chipje, amelyet a grafikon szélein mozgat. A rendőr korlátlan számú zsetonnal rendelkezik, de minimálisra csökkenti a felhasznált zsetonok számát. A rendőr nem tudja mozgatni a zsetonjait, a grafikonon. A játék a következő. A rabló helyezi a chipjét, majd a rendőr azt mondja, hol kívánja felvenni a következő chipet, és a rabló majd áthelyezheti chipét a széleken, de nem a megszállt tetején. A játék akkor fejeződik be, amikor a rendőr a következő chipet a betörő chip tetejére helyezi. Ennek a grafikonnak a mélysége meghatározza a garantált nyereményhez szükséges zsetonok minimális számát [6] [7]. A csillagoknál csak két zseton elég - helyezzük az első zsetont a csillag közepére, arra kényszerítve a rablót, hogy belépjen egy kis sugárba, majd helyezze a második chipet a rabló chipjére. Az n csúcsú útvonal esetében a rendező bináris keresési stratégiát alkalmaz. amely biztosítja a legfeljebb ⌈ log 2 (n + 1) ⌉ (n + 1) \ rceil> chipek használatát.
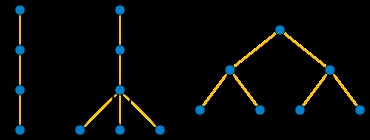
A mélysége a teljes gráf a fa egyenlő a csúcsok száma, és ebben az esetben az egyetlen lehetséges erdő F. úgy, hogy bármely két pontja kell, hogy legyen a szülő-gyerek kapcsolat, egyetlen járható út. Hasonlóképpen, az a fa mélysége teljes páros gráf Kx, y értéke min (x, y) + 1, mintha nem lennének felsők, erdők elhagyja F kell legalább min (x, y) az ősök F. Wood, ahol elért min (x, y) + 1 lehet készítjük, hogy kialakítjuk az utat a csúcsok kisebb arányban a grafikonon, és a csúcsok alkotnak nagyobb arányban a fa levelek F. aljához csatlakozik Apex útját.
Az útpálya mélysége n csúcsokkal pontosan ⌈ log 2 (n + 1) ⌉ (n + 1) \ rceil>. Az ilyen F. mélységű erdőt úgy alakíthatjuk ki, hogy a gyökeret az F út középső pontjába helyezzük, és a gyökér mindkét oldalán két kisebb úton haladunk tovább [8].
A fák mélysége és a fa szélességével való kapcsolat
Az n csúcshoz tartozó erdőnek O (log n) fa mélysége van. Az erdőhöz állandó csúcspontszámot találhatunk, melynek eltávolítását az erdő adja, amely két kisebb al-erdőre osztható, legfeljebb 2n / 3 csúccsal. A két al-erdő rekurzív elosztásával könnyű elérni a fa mélységének logaritmikus felső határát. Ugyanaz a technika, mint a [tree] bomlásának bomlása, azt mutatja, hogy ha a g n-csúcsgörbéjének fa szélessége egyenlő t-vel. akkor a G gráf mélysége O (t log n). [9] Mivel a külső ábrák grafikonok. a párhuzamos egymás utáni grafikonok és grafikonok Halin korlátozott szélességű fákkal rendelkeznek, mindegyiküknek továbbá maximális logaritmikus mélysége van a fáknak.
A másik irányba a gráffa szélessége nem haladja meg a fa mélységét. Pontosabban, a fa szélessége nem haladja meg a grafikon útszélességét [en]. amely legfeljebb egy kisebb, mint a fa mélysége [10] [11].
A G kisebbje egy másik gráf, amely a G részgrafikájából származik, egyes szélekkel. A mélysége a fa monoton a kiskorúak - bármilyen apróbb egy G gráf egy fa mélysége nem haladja meg a mélység a fa a G gráf [12]. Így a Robertson-Seymour-tétel szerint, minden rögzített d esetében a fa mélységű grafikonok száma nem haladja meg a d-t. véges számú tiltott kiskorú.
Ha C a kiskorúak kialakulásával kapcsolatban zárt gráfok osztálya, akkor a C grafikonoknak O (1) fa mélysége van, ha és csak akkor, ha a C nem tartalmazza az összes útvonalat [13].
A fa mélysége szoros kapcsolatban áll a gráf által generált szubgrafák elméletével. Az olyan gráfok osztályában, amelyeknél a fa mélysége nem több, mint d (bármilyen rögzített természetes d esetén), a szubgrafálás által generált tulajdonság teljesen kvázi rendezett [14]. A bizonyítás alapgondolatát, hogy ez a kapcsolat teljesen kvázi rendben van, az indukció használata d-ben. A d magasságú erdõk a d-1 magasságú állványok egymás után értelmezhetõk (a d magasságú fák gyökereinek eltávolításával alakul ki) és a Higman lemma használható. hogy ezek a szekvenciák teljesen kvázi rendben vannak.
Tól egészen kvázi az következik, hogy minden tulajdonság a gráf monoton szülte részgráfok, generálja véges számú tiltott részgráfok, és ezért lehet ellenőrizni polinomiális időben grafikonok korlátozott mélységű fa. A fa mélységét nem meghaladó grafikonok d. maguknak van egy véges számú tiltott generált subgraph. [15]
Ha C a korlátozott degenerációjú grafikonok csoportja [hr]. A C-ban lévő grafikonok korlátozott fa szélességűek, ha és csak akkor, ha létezik olyan útvonal, amely nem jelenik meg generált részgrafikonként a C-ben [13].
A fa mélységének meghatározása összetett számítási feladat - a megfelelő felismerési probléma NP-teljes [16]. A probléma továbbra is NP-teljes a kétpártú grafikonok számára [17]. valamint az akkordgráfokra [18].
Pozitív pillanatokból - a fa mélysége polinom időben számítható ki intervallumgrafikonok esetén [19]. mint a permutációs grafikonok, a trapéz alakú grafikonok, a körkörívek metszésgráfjai, a ciklikus permutációs grafikonok és a korlátozott dimenziók finomsági kötöttségi grafikonjai [20]. A nem orientált fák esetében a fa mélysége lineáris időben számítható [21] [22].
Bodlender, Gilbert, Hafsteinsson Kloks és [10] javasolt egy algoritmust közelítő keresési fa mélysége együtthatója a közelítés C O ((log n) 2))>. Az algoritmus azon alapul, hogy a fa mélysége logaritmikusan függ a gráf szélességétől.
Mivel a mélység a fagráf monoton kiskorúak, a keresési feladat fixen oldható parametrikusan [en] - van olyan algoritmus kiszámításához a mélység egy fa, a munkanap során F (d) n-O (1)>. ahol d az adott gráf mélysége, és n a csúcsok száma. Így minden d rögzített érték esetén a vizsgálatnak meg kell vizsgálnia, hogy a fa mélysége meghaladja-e a d értéket. megoldható polinom időben. Pontosabban - függően n az algoritmus lehet lineáris a következő módszerrel: az épület egy keresési fa mélysége és ellenőrizze nagyobb a fa mélysége 2 értéket ad vagy nem. Ha több, a fa mélysége meghaladja a d értéket, és a probléma megoldódott. Ha nem, akkor lehet, hogy építeni a fa keresést egy sekély mélységben bomlási fa [en] és a szokásos dinamikus programozási technika grafikonok korlátos fa szélessége kiszámításához a mélység a lineáris idő [23].
A fa mélységét pontosan kiszámíthatjuk a grafikonok esetében, amelyek mélysége nagy lehet, egy időben O (cn) egy állandó c értékkel. valamivel kevesebb, mint 2. [24]