Egy irányítatlan grafikon
A grafikonelmélet a matematika egyik területe, amelynek egyik jellemzője a tárgyak tanulmányozásának geometriai megközelítése. A grafikonok és algoritmusok elméletét széles körben használják a programozásban. A gráf fogalma és a kapcsolat fogalma azonos fogalmak. A grafikonelmélet nagyon kényelmes nyelvet biztosít a szoftver modellek leírásához. Képeket lehetővé teszi, hogy azonnal „látott” a dolog lényegét intuitív szinten, kiegészítve és díszítő unalmas racionális szöveges bizonyítékok és bonyolult képletek. A grafikonelmélet első problémái a matematikai szórakozási problémák és rejtvények megoldásával kapcsolatosak.
A grafikonelmélet első munkája Eulernek (1736), bár a "grafikon" kifejezést 1936-ban a magyar matematikus Denech Koenig mutatta be.
A G (V, X) gráf két véges halmaz párja: a pontok és a pár párospontot összekötő vonalak.
A pontok a csúcsok, vagy a gráf csomópontjai, a vonalak élei.
Legyen G (V, X) a grafikon, ahol V = 1. V2 ...> legyen a csúcsainak halmaza, és X (V1, V2) a széle.
Ha az X elemeit rendezetlen párként kezelik, akkor a grafikon nem irányított. és a párokat bordáknak nevezik. Ha az E elemeit rendezettnek tekintjük, akkor a grafikon orientált. és a párok ívek.
Ha a G gráf éle két csúcsához csatlakozik, akkor azt mondják, hogy ez a széle rájuk esik.
A gráf két csúcsa összefüggésbe hozható, ha van egy szélük, amelyik rájuk esik.
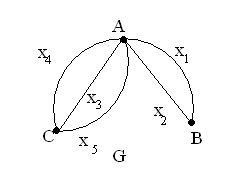
-szomszédos csúcsok - A és B, A és C.
- A és C csúcsokat az x3 peremre
Ha a grafikon olyan élrel rendelkezik, amelynek kezdete és vége egybeesik, akkor ezt az élet huroknak nevezzük.
A G (V, E) gráfnak vannak élei azonos alakú párokkal (X, V, W).
Az ilyen élek többszörösek vagy párhuzamosak.
Az ábrán az x1 (A, B) és x2 (A, B)
Az x (V, W) formájú azonos párok számát az él (V, W) sokféleségének nevezik.
A 3. ábrán az AS széle többszörös, mint 3, és az AB él egy olyan sokaság, amely 2-nek felel meg.
2. Az élek száma esetet a csúcsból az úgynevezett mértéke a vertex és jelöljük C (A) (az angol. Fokozat).
Ha a tetején a hurok eset, hogy hozzájárul, hogy a hatalom két, tehát mindkét végén jön ez a csúcs.
Az ábrán (A) = 5, deg (B) = 2, deg (C) = 3
Egy olyan gráf csúcsát, amelynek nullával egyenlő nagysága van, elszigeteltnek nevezzük.
Az elkülönített csúcsokat tartalmazó gráfot nulla diagramnak nevezik. Az X = t null görbéhez.
Egy olyan gráf csúcsát, amelynek nagysága 1-nek felel meg, függvénynek nevezzük
A G (V, E) gráfban az összes csúcsa fokának egyenértéke egyenlő a görbe éleinek kétszeresével:
ahol n = V a csúcsok száma, m = X a grafikon éleinek száma.
Azt mondják, hogy a csúcs még akkor is, ha mértéke páros szám.
A csúcsot páratlannak nevezik, ha mértéke páratlan szám.
A 3. ábrán a B csúcs egyenletes. és az A és C csúcsok furcsaak.
A grafikon páratlan csúcsainak száma egyenletes.
Következmény. Lehetetlen rajzolni egy páratlan számú páratlan csúcsú grafikont.
4. Egy grafikon, amelyben az összes lehetséges széle nem épül fel, hiányos grafikonnak nevezik
Egy grafikon, amelyben bármelyik két csúcsa egy-egy élével van összekötve, teljes diagramnak nevezik.
A teljes gráfot csak a csúcsai határozzák meg
Ha a teljes gráf n csúcsokkal rendelkezik, akkor lesz
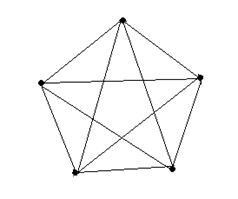
a teljes grafikon a 2. ábrán.