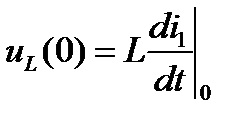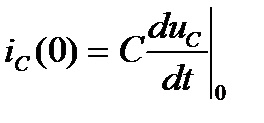Az integrációs állandók meghatározása
A szabad összetevőkre vonatkozó kifejezésekbe lépő integrációk konstansjait úgy számítjuk ki, hogy az ismert kezdeti feltételeket a kívánt függvény és a (n - 1) származékai helyettesítik az adott időre, t = 0+ (n a jellemző egyenlet gyökereinek száma).
A legáltalánosabb esetben, ha a jellemző egyenlet van
n gyökerek, és a tranziens áram vagy feszültség megoldása formában van
. hogy megtalálja az A1 integrációs állandókat. A2, ...... A szükség van egy olyan rendszer összeállítására, amely az alábbi alakú n egyenleteket tartalmazza
Ezekben az egyenletekben a kényszerített komponensek értékei a
t = 0+.
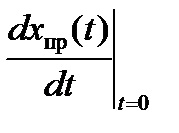
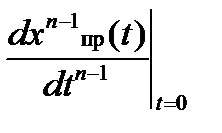
Ha a probléma tranziens folyamatot tartalmaz a DC áramkörben, akkor. és minden származék nulla.
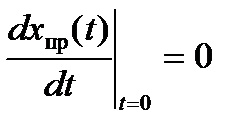
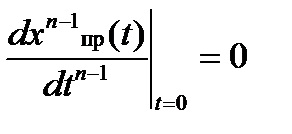
A szinuszos áramkörben a kényszerített alkatrészek a szinuszos törvénynek megfelelően is változnak. Az első származékot a kifejezés adja.
Az idő t = 0.
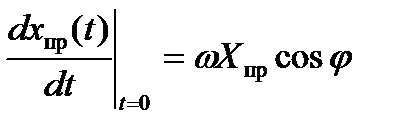
A 2.6. Táblázat mutatja a tranziens áramok vagy feszültségek és az első származékaikat egy tranziens folyamat esetén egy dc áramkörben.
Az integrációs állandók kiszámításához használt egyenleteket a táblázat utolsó oszlopában adjuk meg, ha az átmeneti változó és az első származék kifejezéseiben a t = 0 értéket helyettesítjük.
2.6. Táblázat - Az integrációs állandók kiszámításához használt egyenletek
A tranziens áramokra és feszültségekre vonatkozó kifejezések
A szükséges kezdeti feltételek
Az integrációs állandók kiszámításához alkalmazott tranziens áramok és feszültségek első származékainak kifejezései
Az integrációs állandók kiszámításához használt egyenletek (egy átmeneti folyamat egy állandó áramkörben)
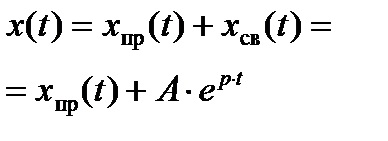
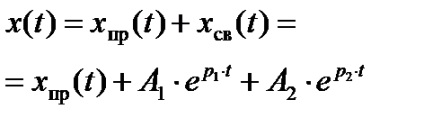
;
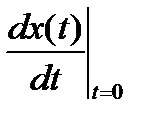
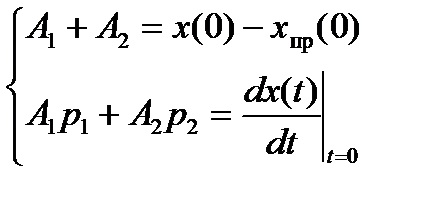
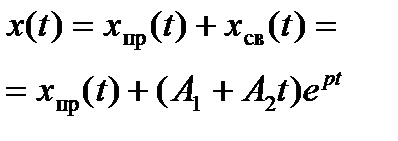
;
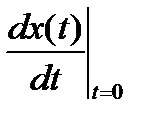
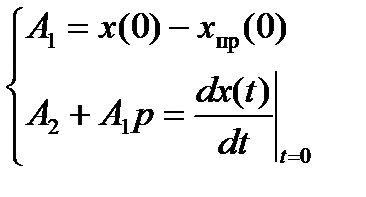
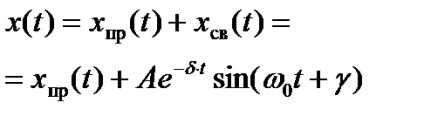
;
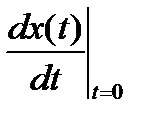
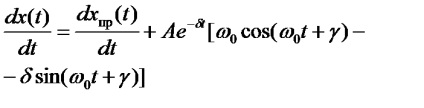
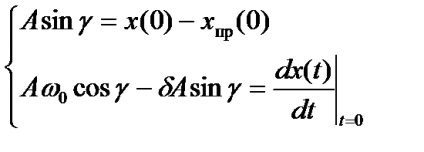
A 2.6 táblázatban szereplő képletek szerinti integrációs állandók meghatározásához először meg kell számolni a kezdeti feltételeket.
A kezdeti feltételek az áramok, feszültségek és származékaik értékei a tranziens folyamat kezdeti pillanatában, at.
A kezdeti feltételek függetlenek és függőek.
A független kezdeti feltételek az induktív elemek áramának értékei és a kapacitív elemek feszültségei
A független kiindulási feltételeket a kommutációs törvények határozzák meg. ; .
Ezek lehetnek nulla és nem nulla.
A függő kezdeti feltételek az összes többi áram, az feszültség és az áramerősség időszármazékainak értékei és az idő függvényei. A függő kezdeti feltételek meghatározása:
- a független kezdeti feltételek kiszámítása után;
- a Kirchhoff-nak a korábban rögzített utómunka-rendszerre vonatkozó egyenleteiből.
A kiszámítandó kezdeti feltételek száma megegyezik az átmeneti érték kifejezésében szereplő integrációs állandók számával. Ahogy a 2.6. Táblázatból következik, ha a jellemző egyenletnek egy gyökere van, és az integráció egy ismeretlen állandója bekerül a szabad áram vagy feszültség kifejezésébe, meghatározásáért először csak egy kezdeti feltételt kell kiszámítani: maga a funkció értéke. Ha az ismeretlen integ- rációs konstansok kettő, akkor két kezdeti körülményt számolnak ki meghatározásukra: a funkció maga és az első származéka
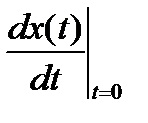
E = 100 V, R1 = 10 Ω, R2 = 10 Ω,
R3 = 10 Ohm. L = 0,1 H
Először, független kezdeti állapotot találunk. ez a rendszer
áram. mivel ez az áram az induktivitáson keresztül. Az első kommutaciós törvény szerint az egyenértékű lesz ugyanazokkal az induktivitással, mint az utolsó kapcsolás előtt.
Az áramkörben történő kommunikáció előtt (2.36. Ábra) egy DC
Ez az áram állandó és az idő
nem függ, így időben
Az első törvény a kommutation
Az induktivitás áramának és áramának fennmaradó ismeretlen kezdeti értékei a függő kezdeti feltételek.
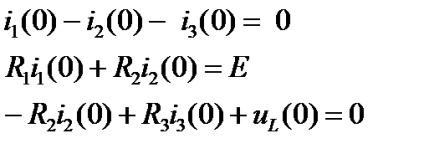
Az ismeretlenek ebben az egyenletben. Ezeket az egyenletek összeállított rendszerének megoldásával bármely Mathcad-módszerrel vagy manuálisan megoldhatjuk, például helyettesítéssel.
Az első egyenletből, amelyet kifejezzük és helyettesítjük a második egyenletbe, kapunk.
2. példa (2.37. Ábra)
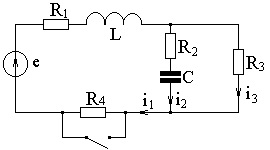
E = 100 V; = 10 Ohm;
= 20 ohm; L = 0,05 H; C = 250 uF.
A kapcsolás előtti áramkörtől kezdve független indítási feltételeket találunk (az induktív áram és a kapacitív elemek feszültsége a t = 0- időpontban). Mivel E = const esetén kapacitív elemen nincs áram, akkor: i1 (0) = i3 (0-) = E / (R1 + R3 + R4) vagy i1 (0) = 100 / (10 + 10 + 20) = 2,5 A,
A függő kezdeti feltételek meghatározásához az egyenleteket Kirchhoff-féle törvények szerint írjuk le a kapcsolási idő után a t = 0+ után:
.
A fenti független indítási feltételeket i1 (0) és uC (0) helyettesíti ezekre az egyenletekre, így: A; A; B.
Az áram deriváltja az induktivitáson keresztül a képletből származik