A folyadékok alapvető tulajdonságai
A folyadékok alapvető tulajdonságai
A hidromechanika az egyensúly és a folyadékmozgás tudománya, valamint a folyadékok szilárd anyagokkal való kölcsönhatása.
A hidromechanika, az általános mechanika ágaként, hidrosztatika és hidrodinamika.
A hidrosztatika esetében a folyadékokat nyugalmi állapotban, a hidrodinamikában - mozgásállapotban vizsgálják.
A hidrodinamikában a könnyű mozgékonyságú (fluiditású) testeket figyelembe veszik. A fluiditású testek képesek szétválogatás nélkül megváltoztatni alakjukat a kisebb erők hatása alatt. Az ilyen testeket folyadéknak nevezik.
A folyadék a hidromechanikában folyékony és gáznemű közegeket jelent, mivel közös tulajdonságaik vannak, és a megfigyelt jelenségeket ugyanazok a függőségek írhatják le. Azonban vannak különbségek a folyékony cseppek és a gázok között:
1. Az intermolekuláris kölcsönhatás jelentõs erõi szabad felületek formájában. 2.Pool tömörítve.
1. Nincs intermolekuláris kölcsönhatás, így szabad felületek nem alakulnak ki, de teljesen elfoglalják a térfogatukat, amelyben találhatóak. 2. Nyomja jól össze.
A folyadék fő mechanikai tulajdonságai:
A folyadék tömegét a fajlagos gravitáció jellemzi - a folyadék p tömegének aránya a foglalt térfogatig v
A folyadék sűrűsége a folyadék m tömegének a térfogatához viszonyított aránya. V
A sűrűséget és a fajsúlyt a függőségek okozzák # 947; = # 961; g, ahol g = 9,81 m / s 2 - a gravitáció gyorsulása. A hajó számításai szerint:
friss vízhez # 961; = 1,0 t / m 3 (102 kgf # 903, s 2 / m 4), # 947; = 9,81 kN / m 3;
a standard sűrűségű tengervíz esetében # 961; = 1,025 t / m 3 (105 kgf # 903; s 2 / m 4), # 947; = 10,06 kN / m3;
levegőre # 961; = 1,225 kg / m 3 (0,125 kgf # 903, 2 / m 4), # 947; = 12,02 N / m 3.
A felületi feszültséget egy folyadék tulajdonságának nevezik, amely a molekuláris kohéziós erők hatására további nyomást gyakorol a szabad felületre. A folyadék e tulajdonságát a felületi feszültség koefficiense jellemzi # 945;
A viszkozitás a folyadék képes ellenállni, ha az egyik része a másikhoz képest csúszik. Az F belső súrlódási erő arányos a folyadék sebességének változásával # 965; a mozgással merőleges irányban, és attól függ, hogy a folyadékelemek érintkezésben vannak-e
Ez Newton viszkózus súrlódásának törvénye. Az arányossági együtthatót az úgynevezett dinamikus viszkozitás együtthatója - # 956; (Pa # 903; c).
A dinamikus viszkozitás együtthatójának és a folyadék sűrűségének arányát a kinematikus viszkozitás koefficiensének nevezzük
A kinematikus viszkozitás együtthatója a hőmérséklet függvénye. 20 ° C-os vízhőmérséklet esetén 1 # 903, 10 -6 m 2 / s levegő esetén - 1,5 # 903, 10 -5 m 2 / s.
A hidrostatika tanulmányozza a folyékony közeg egyensúlyi szabályait, valamint a folyadék és a szilárd anyagok közötti kölcsönhatást. olyan helyzetekben, ahol nincs mozgás vagy a sebesség elhanyagolható.
A hidrostatika lehetővé teszi egy ilyen fontos hidrodinamikai mennyiség bizonyos tulajdonságainak megértését, mint nyomás. A szilárd anyag nyomását súlya határozza meg, a folyadék nyomása a mélysége. A p-edény aljának nyomóereje (1. ábra, a) nem függ a forma alakjától, hanem csak az edénybe öntett folyadék szintje alapján határozható meg a hidrosztatikus képlet szerint:
ahol # 961; - a folyadék sűrűsége, és a P0 - folyadéknyomás a rögzített szinten (szabad felületén hozzáférhető - légköri nyomáson), h - lag a függőleges ezen a szinten addig a pontig, vizsgált (merülési mélység), ri - gauge (gauge) nyomáson.
Szilárd anyaggal érintkezve a folyadék nyomást gyakorol rajta, normál irányban a test felületére irányítva. A felesleges folyadéknyomás erőssége egy sík felületen, amelynek függőleges szimmetriatengelye van (1, b ábra)
ahol hc a függőleges távolság ct. a felület a folyadék szabad felületének szintjétől; S a felszíni terület.
1. ábra. Hidrosztatikus nyomás és folyadéknyomás.
A felszínen keletkező nyomásnyomok alkalmazásának D pontja, a nyomás központ (centiméter), a távolság a ct-től. terület (C) l távolságban.
A görbületi felületre gyakorolt túlnyomás (1, c ábra) az Fx komponensei alapján határozható meg. Fy és Fz. a koordináta tengely mentén
Az ívelt felületen lévő nyomóerő (Fx vagy Fy)
ahol hcv a függőleges távolság a hidrosztatikus fej függőleges síkjától (1. és c. ábra).
A Fhor erővonal áthalad a Dvert függőleges vetület területének D nyomásának közepén.
A függőleges összetevője a görbe felület a nyomóerő megegyezik a folyadék tömegének henger által határolt alsó felülete és a felső síkja a hidrosztatikus (2a ábra) áthalad CG térfogata
A hajlított felületen lévő prizmát nyomás alatt álló testnek nevezik.
A W nyomásméret térfogata nem feltétlenül egyezik meg a hajó tényleges térfogatával. Ha a folyadék ívelt felület alatt van, akkor a nyomásmérő testének térfogatát a felszín felett lévő térfogat határozza meg a hidrosztatikus fej síkjára, és az erő függőlegesen felfelé irányul (2.
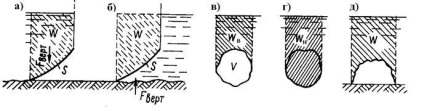
2. ábra. Nyomáserő a görbületes felületeken.
Amikor a test úszik a folyadék felületén, a nyomásmérő test térfogata megegyezik az általa elmozdított víz térfogatával, térfogat elmozdulás (2c ábra, d)
Amikor a test teljesen elmerül a folyadékban, a felülete felsõ felének nyomásának testtérfogata megegyezik a WB-vel. és az alsó Wn.
A vertikális összetevőt ilyen esetekben az elszívó erőnek nevezik (a lebegő testekre, a fenntartás erejére vagy a felhajtóerőre)
Ennek eredményeképpen Archimédész törvényt kapunk: olyan erő, amely a vízbe merülő testre hat, amely az általa eltolódott víz súlyával egyenlő, és függőlegesen felfelé irányul. Ennek az erőnek a vonala átmegy az eltolódott térfogat súlypontján.
Az archimédesi törvény a szokásos formában nem alkalmazható a testfelületekkel érintkező felületeknél, amelyek között a folyadék nem tud behatolni. Egy ilyen testnek csak egy erőfeszítése van a folyadék részéről # 961; gW, nyomja meg a talajra (2. De amint egy folyadék szivárog a felületre, egy erő kikényszeríti a testet.
A hidrodinamika egy fluidum mozgását vizsgálja, amely stabil és instabil.
A mozgást állandónak nevezik. Ha a mozgó folyadék által elfoglalt hely minden egyes pontján,
A növekedés nem függ az időtől, és ezért állandó marad. Ellenkező esetben a mozgás bizonytalan.
A folyadékmozgás természete lehet lamináris és turbulens. A lamináris folyadékmozgás olyan mozgás, amelyben nincs sebesség pulzálással, ami a részecskék összekeveréséhez vezet. Ha a folyadék mozgása az áramlás részecskéinek keveredését okozó sebességek pulzálásával történik, akkor az ilyen mozgást turbulensnek nevezzük.
A hidrodinamikában az aktuális vonalak fogalmát használják. Az áramlási sebesség vektorához tartozó áramvonalak vonalai. A folyadék állandó mozdulata miatt a folyadék részecskéinek mozgása és mozgásai egybeesnek egy nem folyékony folyadékkal, és nem esnek egybe.
A zárt áramkörön áthaladó áramvonalak által alkotott felületet az aktuális csőnek nevezik; a folyadékcsövet, amely megtöltötte az áramcsövet, - egy elemi áramot.
Az áramvonalak vizuális ábrázolását a levegő áramlása a sík fölött egyenletes légáramlással veszi figyelembe. A 3. ábrából. Látható, hogy az aktuális vonal alja nem nagyon torzult, ott az áramlási sebesség növekedése elhanyagolható. A szárny felső oldala sokkal inkább megváltoztatja a levegő áramlását - ott az áramvonalak összenyomódnak, és a sebesség sokkal nagyobb, mint az áramlás maga.
3. ábra. A szárnyak egyenletesen áramlanak. Az egyenlet származtatásához
levegőáramlás. Bernoulli.
Sokkal nehezebb leírni egy folyadék mozgását, mint megoldani a hidrosztatika problémáit, ezért a folytonosság egyenleteit és a Bernoulli-egyenletet széles körben használják a hidrodinamikában.
A folytonosság egyenlete a tömegek megőrzésének törvényét fejezi ki, és a következő formában használatos:
itt # 965; - a folyadék sebessége, S az aktuális cső keresztmetszete, Q a térfogatáram. A törvényt az alábbiak szerint lehet megfogalmazni: a jelenlegi cső bármelyik keresztmetszeténként egységnyi idő alatt azonos mennyiségű folyadék áramlik.
A hidromechanika egyik legfontosabb egyenlete Daniel Bernoulli (4. Ő volt az első, aki leírta az elnyomhatatlan ideális folyadék mozgását (a súrlódási erők az ideális folyadék elemei között, valamint az ideális folyadék és a hajó falai között nincsenek jelen). A Bernoulli-egyenletnek az a formája:
p + # 961; # 965; 2/2 + # 961; gh = const,
ahol p a folyadéknyomás, # 961; - sűrűsége, # 965; - mozgássebesség, g - gravitációs gyorsulás és h - magasság, amelyen a folyadékelem található. A Bernoulli-egyenlet kifejezi az energiatakarékossági törvényt és az ideális folyadék áramlásának folytonossági állapotát.
Ebben az egyenletben minden kifejezésnek van egy nyomásmérete, és ezeket nevezik:
p a statikus nyomás;
# 961; # 965; 2/2 - dinamikus nyomás;
# 961; gh - súlynyomás.
Megfigyelhető, hogy a sebesség hiányában a Bernoulli-egyenlet hidrosztatikus formula lesz. A sebességváltozás a Newton második törvényének megfelelően olyan erő hatására történik, amely a folyadékra ható, ebben az esetben a gravitáció vagy a nyomáskülönbség a folyékony folyadék térfogatára hat.
A Bernoulli-egyenletben két kifejezés található:
# 961; # 965; 2/2 a mozgó folyadék egységnyi térfogatának kinetikus energiája és # 961, gh a folyadék egységnyi térfogatának potenciális energiája,
pontosan ugyanúgy, mint egy anyagpont energiatakarékossági egyenletében. Specificitás nyilvánul hidromechanika nyomás jelenlétében p - nyomásesés különböző részein az áramlási cső következtében a folyadékot mozgatni, hogy a gyorsulás, és ezért amellett, hogy a Bernoulli képlet, a kinetikus és a potenciális energia egységnyi térfogatú folyadékot még jelen, és a vérnyomást.
Következésképpen, ha a cső (vagy áramlási cső) van elrendezve úgy, hogy a nyomás abban állandó marad, a Bernoulli-egyenlet a folyadék csak egybeesik a törvény az energiamegmaradás az anyagi pont. Ha a cső úgy van kialakítva, hogy nem lehet figyelembe venni a változás h magasság (mivel a kis sűrűségű anyag, vagy egy kis változás ebben a magasság), összhangban a kontinuitási egyenlet a sebesség a szűk szakaszok a cső növekszik - így a nyomás is van, hogy esik. Ez természetes eredmény, mivel a sebesség (gyorsulás) növekedését csak a nyomásesés biztosítja, és a nagy sebességű helyeken a nyomásnak kicsinek kell lennie.
A Bernoulli-egyenlet egyszerűen megmagyarázza a "hajóelmélet" során figyelembe vett számos jelenséget. Például egy olyan szárny, amely egyenletes vízáramlás körül áramlik, akár támadásszög hiányában is, emelkedő ereje van. Az egymással párhuzamos járatokon közlekedő hajókon a hidrodinamikus erő hat, egymás felé tolva. A hajócsavar gyors elforgatásával létrejövő nagy folyadékáramlások kavitációt okoznak. képes megdönteni a pengéit. A késleltetés működésének alapelve a Bernoulli-egyenleten alapul, amely lehetővé teszi egy folyadék sebességének mérését.