Poligonok, matematika
77. Már meg kellett építeni négyszögeket (50. bekezdés). Most bővítjük ezt az építést. Adjunk 4 pontot: A, B, C és D [cher. 84 (I)]; a 4 pontot párhuzamosan összekötő összes lehetséges közvetlen vonalat építjük - feltételezzük, hogy ezek közül a pontok közül 3 nem található ugyanazon a vonalon. Az ilyen sejtvonalak képesek az összes építeni 6 (minden egyes pont a másik három 3 vonal, pontokként 4, a teljes közvetlen 3 * 4 = 12, de minden sor kell tekinteni két-szeres, például a direkt AC :. Ha már úgy vélte elérte A-tól C-ig, és néha C-től A-ig, így a különböző vonalaknak (4 * 3) / 2 = 6) kell lenniük. Az így kapott szám 4 pontból és 6 sorból áll, amelyek párban összekapcsolják őket - ez teljes négyszög. Mind a négy pontot a csúcspontnak nevezik. És minden egyes vonal, amely belép, az ő oldala. a teljes 4-gónak 4 csúcsa és 6 oldala van.
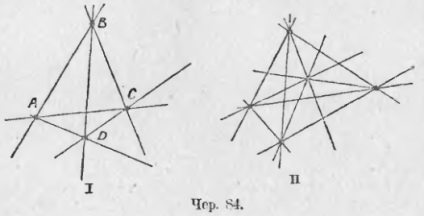
Ha 5 pontot veszünk (84-es sáv), hogy egyikük ne legyen egy sorban, és páronként összekapcsoljuk, akkor teljes 5 gont kapunk; 5 csúcsa és 10 oldala van. A teljes 6-gónak 6 csúcsa és 15 oldala van, és így tovább.
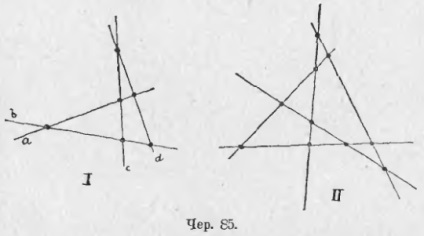
Éppen ellenkezőleg, 4 egyenes, a, b, c és d (85 - I) egyenes vonalat hozhat létre, hogy egyikük sem hágjon át egy ponton, és keresse meg a metszéspontjukat. Tegyük fel, hogy nincsenek pár párhuzamos vonalak az a, b, c és d vonalak között; akkor mindegyik vonal három ponttal három pontra metszi, és az egész keresztezési pont 3 * 4 = 12, de itt mindegyik pontot kétszer megszámoltuk: például egyszer, az a vonal metszéspontjától a vonallal b, a másik pedig a b vonal metszéspontjától az a vonallal; ezért a különböző keresztezési pontok számának 4 * 3/2 = 6-nak kell lennie. Az így létrejövő, négy egyenes vonalból és a kereszteződésük 6 pontjából álló számot teljes négyszögnek nevezik; minden sort az oldalának neveznek, és minden pont a csúcspontja. A négyszög 4 oldal és 6 csúcs. Ha ugyanazt az építést végezzük 5 egyenes vonallal, akkor egy teljes pentagon (85 - II) kapunk. Ha feltételezzük, hogy az 5 egyenes vonal között nincs pár párhuzamos, 5 oldal és 10 csúcs. A teljes hattagú (ugyanazon fenntartással az egyenes vonalakon) 6 oldal és 15 csúcs stb.
78. Vegyünk még néhány pontot, és párokkal összekötözzük őket, de nem mindegyiküket, de először meghatároztuk sorrendjüket, mindegyiket később (az utóbbi az elsővel). Az így létrehozott számot úgynevezett: egy egyszerű sokszög - a fekete. 86 képpontnyi egyszerű 5-as és 6-gonosz képet ad.
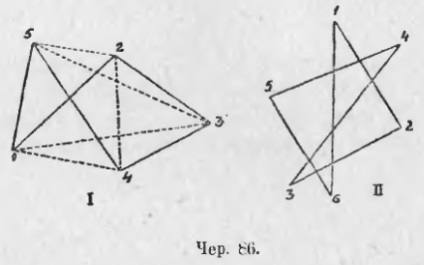
A rajzpontok sorrendjét számokkal jelöljük: itt szükséges, hogy a három szomszédos pont ne feküdjön egy sorban. Minden pont, amely része egy egyszerű sokszög nevezik csúcsa és minden sor - az ő oldalán (tudjuk itt, mint volt a háromszög, hogy megértsük ezen a néven csak egy összekötő szakasz két szomszédos csúcsot a sokszög). Nem nehéz látni, hogy annyi oldal van, mint egy egyszerű sokszög, mint csúcspontok. Ha közvetlenül kapcsolódik a két nem szomszédos csúcsok, majd a kapott vonal (vagy szegmenst, hadifogságba csúcsok között) egy diagonális a sokszög. A fekete. A 86 (I) -et egy egyszerű pentagon átlóinak szaggatott vonalával 5 képezi. Egy egyszerű hatszögben 9 átlós felépítésre van lehetőség (a 86 - II vonalon nem épülnek fel). Mivel egy egyszerű sokszögnek annyi oldala van, mint a csúcsok, ezeket egyszerű multiplikátoroknak is nevezhetjük (egyszerű pentagon stb.). A fekete. A 87. és a 88. oldalon még mindig léteznek különféle egyszerű sokszögek.
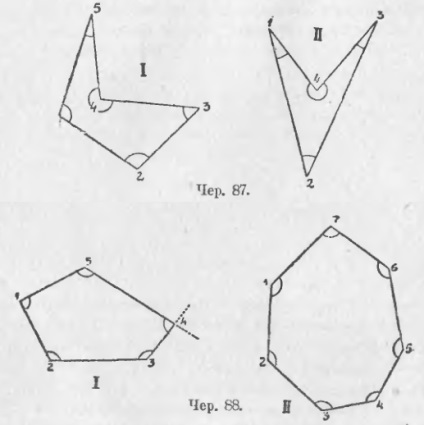
79. Az elemi geometria során csak az egyszerű sokszögeket veszik figyelembe, ezért gyakran szónak nevezik sokszögnek. Az építési egyszerű poligonok lehet két esetben: 1) az a sokszög oldalainak, ami azt jelenti, hogy a név a vonalszakaszok két csomópont között metszi egymást (lásd június 86), és a 2) nem keresztezik egymást (jún 87. és 88.) .... E két eset között jelentős különbség van. Míg a második esetben azt látjuk, hogy a sokszög kiválasztja a síkjából annak bizonyos részét, amely az úgynevezett sokszög területe, az első esetben azt látjuk, hogy vannak több részből - ez különösen észrevehető június 86, II, - és néha két ilyen rész is megkülönböztethető, hogy egyikük egymásra helyezkedik; itt tehát nem látjuk azonnal a területet. amelyet ez a sokszög határol. Ezért a második esetnek (87 és 88 köröknek) megfelelő poligonokat fogunk hívni. és az első esetnek megfelelő sokszögek (86. ábra) - nincsenek területük (ezeket csillagokként is nevezik).
Meg kell jegyeznünk, hogy ha több olyan feltételt teszünk, amelyek lehetővé teszik, hogy a sík egyes részeit pozitívnak vagy negatívnak tekintsük, feltételezhetjük, hogy minden sokszögnek van egy területe. A csillagminták területének kérdése nem szerepel az elemi geometria folyamán.
Gyakran előfordul, hogy a sokszög úgynevezett peremét veszik figyelembe; Ez a név a sokszög összes oldalának összege.
80. Az elemi geometriában szinte kizárólag a területet tartalmazó sokszögek tekinthetők. Az ilyen sokszög csúcsain minden egyes négyszöggel négyszöget kapunk, ha a sokszög oldalán végtelen vonalakat értünk (például lásd az I pentagon 4 csúcsánál lévő 88-os szögeket). Az egyik ilyen sarkok, amelyeknek a belső területe megragadja a sokszög területét, az úgynevezett belső; a sokszög minden csúcsán egy belső sarok érhető el (a belső 87 és 88 belsejében a belső szögeket ívek jelölik).
Ismét ott van egy olyan terület, amelynek két csoportja van: 1) a poligon mindegyik belső sarka kisebb, mint a korrigált szög, - ilyen poligonok konvexek (lásd 88); 2) előfordulhat, hogy egy vagy több belső szög nagyobb, mint a kiegyenesített szögek (87-es szögben mindkét poligonnál a 4. csúcsnál), ilyen sokszögeket nemkonvexnek neveznek.
A domború sokszög rendelkezik azzal a tulajdonsággal, hogy minden csúcsa az egyik oldalán helyezkedik el (ez a név egy végtelen vonalat jelent). A nem konvex poligonnak nincs ilyen tulajdonsága.
A jövőben elsősorban konvex sokszögekkel kell foglalkoznunk.
81. Elsődleges feladatunk a sokszögek megtalálásában, hogy megtaláljuk a sokszög belső szögeinek összegét.
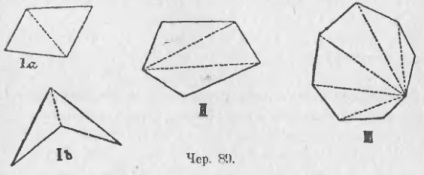
Ha négyzetet veszünk, amelynek területe [ 89, I (a) vagy I (b)], és a kivitelezést egyik átlója - ha az (a) közömbös, amely abban az esetben, I (b), az egyik, hogy található olyan terület négy oldalú sokszög (belül ), akkor két háromszöget kapunk. A 2d háromszög belső szögeinek összege tehát a 4-gon = 2d * 2 = 4d belső szögeinek összege. Ha bármilyen 5-gont veszünk és két átlósat készítünk, amelyek az egyik csúcsából származnak (89-es, II. Szám), akkor 3 háromszöget kapunk; összegeként a belső háromszög szögeinek = 2d, akkor az összeg a belső szögek egy 5-gon = 2d * 3 = 6d; arra is, hogy 6-gon háromszög 4, és ezért az összege a belső szöge = 2d * 4 = 8d és t. d. Ha veszünk, például. 11-gon, majd az átló átépítése után 9 háromszöget kapunk. A 11-gon = 2d * 9 = 18d belső szögeinek összege. Általában, ha vesszük az n-gon, megépítése után átlóinak egyik csúcsainak kapjuk (n - 2) háromszög, és így az összeg a belső szögek a sokszög képlete:
ahol n a sokszög oldalainak vagy csúcsainak száma.
82. A második kérdés a sokszög külső szögének összege lesz. Az úgynevezett „külső sarok” lehet érteni, mint már tette a háromszög, a szög áll folytatása egyik oldalán a sokszög a következő felek (∠I, ∠II és így tovább. D. jún. 90). Menjünk körbe a sokszög oldalán, amelyet például konvexnek fogunk tekinteni. A nyíl által jelzett irányba, mindkét oldalon ugyanabba az irányba halad. Ezután megkapjuk számos külső szögek: ∠I, ∠II stb Tekintsük először a egy pár sarkok: .. A belső és a külső egy közös vertex, pl. ∠1 és ∠I; akkor azt látjuk, hogy összegük egy korrigált szög,
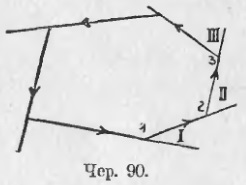
A másik csúcson is megtaláljuk: ∠2 + ∠II = 2d stb. Ha feltételezzük, hogy a sokszög csúcspontja n, az ilyen szögpárok is n, és így:
(Belső szögek összege) + (a külső szögek összege) = 2d * n
De ezt tudjuk
a belső szögek összege 2d (n - 2).
A külső szögek összege = 2dn - 2d (n - 2) = 2dn - 2dn + 4d = 4d
azaz egy konvex sokszög külső szögeinek összege nem függ a sokszög oldalától (vagy csúcsaitól), és mindig 4d.
83. Függelék. A "külső sarok" nevét más értelemben is meg lehet érteni. Tegyük fel, hogy van egy sokszög (fekete 91), amelynek van egy területe, bár nem konvex. Ezután egy külső szögben megérthetjük a sokszög oldalai által létrehozott szöget, nem pedig a hosszabbításokat, hanem a belső sarokat is, ∠ BAC, de a belső területére, vegye azt a síknak azt a részét, amelyet a szög oldalai választanak ki, amely nem tartalmazza a sokszög területét. Az egyes sarkok belsejét a rajzon ívvel jelöljük. Ezután minden ilyen szög, a megfelelő belső szöggel együtt, 2 korrigált szög vagy 4d. belső ∠BAC + külső ∠BAC = 4d.
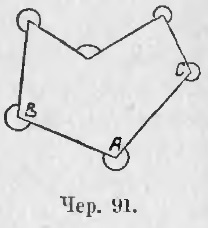
Ha a felek a sokszög N, összege az összes belső és az összeg az összes külső = 4d * n, és így mennyiségű külső szögek = 4DN - 2d (n - 2) = 4DN - 2dn + 4D = 2dn + 4d = 2d (n + 2).
- Teljes hatszög létrehozása. Hány oldala van?
- Hozza létre a teljes hatoldalt úgy, hogy ne legyen párhuzamos oldala. Hány csúcs van?
- Keresse meg a teljes n-gon oldalainak számát és a teljes n-támogató csúcsainak számát (feltételezve, hogy az utóbbi nem rendelkezik párhuzamos oldalakkal).
- Hány átmérőt lehet létrehozni egy egyszerű n-gon csúcsából?
- Hány átlós egy egyszerű n-gont?
- A konvex pentagon minden belső sarkában a derékszögben kell kifejezni, ha minden szöge egyenlő egymással.
- Az előző feladat ötszögére fejezze be a külső szögeket a derékszögben.
- Egy egyenlő háromszögben, minden szög a bázisnál = ¾d. Keresse meg (a derékszögben lévő részekben) a szöget a csúcson.
- Egy egyenlő háromszögben a csúcsszög 5/8 d. Keresse meg a szöget az alján.
- Konvex négyszögben az ellentétes szögek egymással párhuzamosak. Annak megállapítása, hogy egy ilyen négyszög párhuzamos.