A fémtechnológiák és a hegesztés ellenőrzése - vizsgálati munka, 2. oldal
A diszlokációkat lineáris tökéletlenségeknek vagy egy-dimenziós hibáknak nevezik a valódi fémek kristályrácsjainak, amelyek a kristályszerkezet speciális sérülései, amelyek a valós kristályok ideális szerkezettől való eltéréseihez kapcsolódnak.
A diszlokációk élek, csavarok és vegyes görbületűek. Fémek keletkeznek a kristályosodás, a műanyag deformáció és más okok miatt, ami a kristályrácsban a stressz-mezők létrehozását eredményezi, ami a megfelelő helyi deformációkhoz és elmozdulásokhoz vezet.
A diszlokációs elmélet lehetővé tette annak magyarázatát, hogy a fémek valódi ereje miért különbözik az elméleti erősségtől (számításba véve az interatomikus kölcsönhatás erőit).
Képzeljük el, hogy valamilyen oknál fogva az atomok egy további fél síkja megjelent a kristályrácsban, az úgynevezett extra sík Q-ben (1.4. Ábra). Az ilyen sík 3-3 'éle a rács lineáris hibáját (tökéletlenségét) képezi, amelyet perem diszlokációnak neveznek. Ha egy ilyen diszlokáció a csúcson van, akkor azt pozitívnak tekintjük és χ; Az alsó (negatív) alatti peremeltérést a ý jel jelöli.
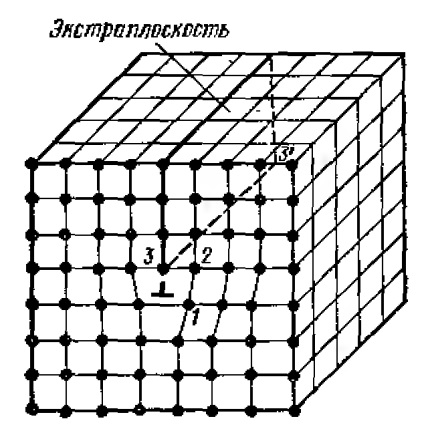
1.4. Ábra. Diszlokáció a kristályrácsban.
A peremhomlokzatok hossza kiterjedhet több ezer rácsos periódusra, a vonal nem lehet egyenes, felületi feszültséggel pedig a kontúrba szorul. A diszlokáció körül a rács elasztikus torzításának zónája keletkezik. A diszlokációk szélessége, vagyis a hiba közepétől a torzítás nélküli rács helyéig terjedő távolság kicsi és egyenlő több interatomikus távolsággal.
Mivel a rács torzulás a diszlokáció közelében az utóbbi könnyen eltolható jobbra vagy balra a semleges helyzetből, és kommunikálni a határ atomjaik 3 atom 1 (lásd. Ábra. 1.4), és szomszédos a jobb (bal) félsíkon áthelyezik majd a közbenső helyzetben, esztergálás .. ezáltal zavar az extra és a széle mentén atomok 2, stb Így, a diszlokáció lehet mozgatni (vagy inkább - továbbított a átjátszó) mentén csúszó síkkal, amely merőleges a az extra STI Q.
A fémek diszlokációját elektronmikroszkóppal megfigyelhetjük.
Elméletileg, az elemi műanyag nyírási (ábra. 1,5), figyelembe véve a atomok közötti erőkkel, minden egyes pár konjugátum atomok (viszonyítva a csúszó síkra AA), 1-1”, 2-2' és t. D., és tekintve, hogy a csúszás síkjában a valódi fémkristály hozzávetőlegesen 1014 atom per cm 2 keresztmetszetű, szükség rendkívül nagy erőt (technikai vas, amint azt említettük, tízszer nagyobb, mint a ténylegesen megfigyelt).
A diszlokáció elmélet szerint a fémben lévő műanyag nyírást a diszlokációk relé mozgásának folyamataként kell tekinteni. E folyamat egyszerűsített diagramját az 1. ábra mutatja. 1.6.
A diszlokáció jelenlétének következtében (23a. Ábra) a kristályrács torzított állapota megjelenik az AA csúszás mindkét oldalán a kristályban, az atomok közötti ideális kötések sorrendjének megzavarásával. Ebben az esetben elegendő egy kis P külső erő alkalmazása (sokkal kisebb, mint a P erő egy ideális rácshoz, 1.6b ábra), amely
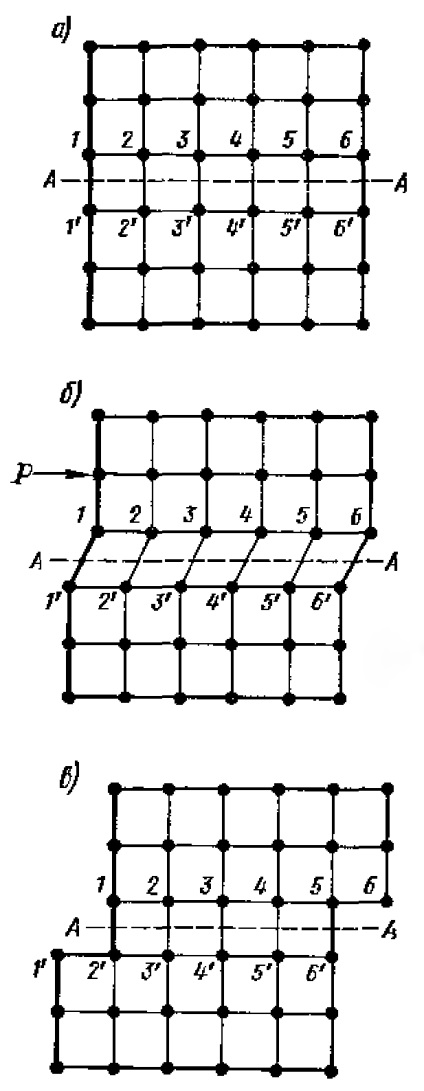
1.5. Ábra. Műanyag nyírás egy ideális kristályrácsban:
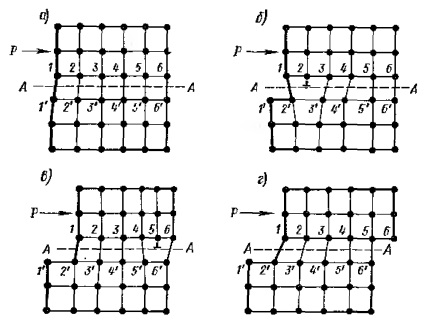
1.6. Ábra. A műanyag nyírási mozgási sémája.
a függőleges atomvonalak egymást követő részleges elmozdulásának hulláma az AA csúsztató sík felett, amely nem haladja meg az egyik interatomikus távolság értékét. E hullám áthaladásának eredményeképpen a diszlokáció, mint egyfajta relé faj, egymás után átkerül a 3 és 4 atomok soraira. Néhány ponton a 3. ábrán bemutatott helyzet. 1.6V. Az atomok egy adott elmozdulásából származó mozgás átvitelének eredményeképpen 1 a diszlokáció felszíni és eltűnik, amint az az 1. ábrán látható. 1,6 g. Így a diszlokáció elmozdulása végeredménye az AA csúszási sík mentén az egyik interatomikus távolság eltolódása volt, és sokkal kevesebb erőfeszítésre van szükség a műszak végrehajtásához, mint diszlokáció hiányában.
Ebből levonhatjuk azt a következtetést, hogy a kristályban való eltolódás könnyebb, annál nagyobb a helyük a fémben. Épp ellenkezőleg, annál kisebb az ilyen diszlokációk száma egy fémben, annál kisebb nyírási lehetőségek és annál erősebb a fém. Egy olyan fémben, amelyben nem alakul ki eloszlás, a váltás csak a kristály egyik részének egymás utáni elmozdulása (a teljes egészében) a másikhoz képest lehetséges.
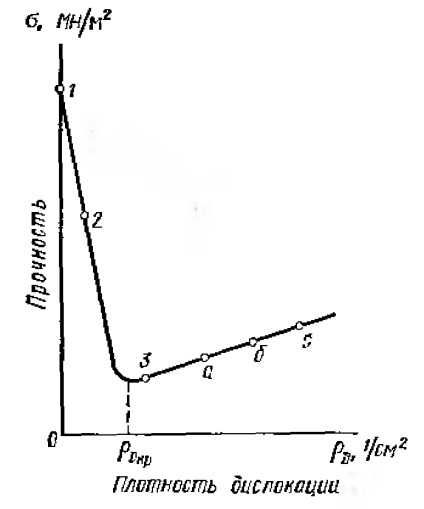
Ebben az esetben a diszlokációmentes fém erősségének meg kell egyeznie az elméleti értékkel (az 1. ábra 1. pontja). Tartóssági huzaiszerű kristály - úgynevezett bajuszát (2. pont a 1.7 ábra.) - közel volt az elméleti értéknek, hogy megfelelően a feltételezést, mivel igen kis számú diszlokációk. Például fonalszerű vas-kristályok esetén a szakítószilárdság 140 MN / m2 (MPa).
A fém szilárdságának nagymértékű növekedése a kristályszerkezet tökéletességének növelésével (a bajuszok példáján) meggyőző megerősítése a diszlokációelméletnek.
A diszlokációmentes fémkristályok megszerzése mellett van egy másik módszer a fémek keményítésére. Kiderül, hogy a fémek valódi ereje csak az elején növekvő számú diszlokációval csökken. Miután elérte a legkisebb értéket a diszlokációk bizonyos kritikus sűrűségéhez (1.7. Ábra), az igazi erő ismét növekedni kezd. A valódi erő növelésével, a növekvő diszlokációs sűrűséggel magyarázható, hogy nemcsak a párhuzamos eltérések merülnek fel, hanem a különböző síkok és irányok közötti eltérések is. Az ilyen diszlokációk megakadályozzák egymás mozgását, vagyis egyre több atom vesz részt a műanyag deformáció elemi aktusában, és a fém igazi ereje megnő.
Hagyományos módszerek keményedő fém, ami növeli a diszlokációsűrűség mechanikus munka keményedés, és szemcsefinomító teljes fragmentáció kristályok eredményeként hőkezelés. Néhány régóta ismert adalékolás technikákkal (például, beépítése a rács az alapfém idegen atomok), ami mindenféle tökéletlenségek és a torzítás a kristályrács, megakadályozzák a szabad mozgását diszlokációk, vagy blokkolja azokat. Ez magában foglalja az úgynevezett erősítő fázisok (pl. Diszperziós keményedés) szerkezeteinek kialakítására szolgáló módszereket is.
Mindazonáltal ezeknél az esetekben a keményedés nem éri el az elméleti értéket. Következésképpen bizonyos mértékig a valódi fémkristályban lévő diszlokációk jelenléte az oka annak, hogy erőssége csökken, mivel az elméleti szinten alacsonyabb feszültségeknél plasztikusan deformálódhat.
Meg kell jegyezni, hogy a diszlokációk egymással és más fémhibákkal való kölcsönhatása olyan összetett, hogy egyszerű diszlokációs elméletek alapján nem lehet megjósolni a szilárd anyagok erejét. A diszlokációk elmélete azonban lehetővé teszi a szilárd anyagok deformációjának, törésének és keményedésének folyamatainak minőségi jellemzését.
A diszlokáció elmélete a szilárdtestfizika és a fizikai kohászat részévé vált. A fémekben és ötvözetekben előforduló valamennyi folyamat, valamint tulajdonságaik kialakulása elválaszthatatlanul kapcsolódik a kristályszerkezetben fellépő hibák jellegéhez és sűrűségéhez, és elsősorban a diszlokációhoz. Tehát a plasztikus deformáció, amely rendszerint egy intragranuláris eltolás, megvalósul, amint azt korábban említettük, a diszlokációk mozgásával.
A diszlokációk elmélete megmagyarázza a törzsek és a feszültségek közötti összefüggést, feltárja a törzs kikeményedésének okait (a munka keményedése). Minél nagyobb a diszlokáció sűrűsége egyenletes eloszlással, annál nagyobb a fém szilárdsága.
A szilárd oldatok keményítése nem magyarázható anélkül, hogy figyelembe kellene venni a feloldódott atomok kölcsönhatását a kristályszerkezetben lévő hibákkal, és elsősorban a diszlokációkkal.
A diszlokációk körül keletkezhetnek idegen atomok klaszterei, "Cotred atmoszférái". Az ilyen klaszterek (különösen az intersticiális atomok) kialakulása nagymértékben akadályozhatja a diszlokációk mozgását, ezáltal növelve a műanyag deformációs ellenállását.
A fémek megsemmisítésének folyamata nem magyarázható anélkül, hogy a diszlokációk elméletén alapulna, mivel a pusztulás és a műanyag deformáció elválaszthatatlanul összekapcsolódott. Javasoltak különféle diszlokációmodelleket a repedésmagok kialakulására, amelyek a korlátok előtt elhelyezkedő diszlokációk felhalmozódásából származnak.
Anélkül, hogy a diszlokáció elméletére hivatkoznánk, nem lehet megmagyarázni a fémek kúszását, mivel ezt a diszlokációk csúszó és "kúszó" folyamata határozza meg.
A diszlokációk jelentősen befolyásolják a diffúziós folyamatot. Mivel a diszlokációk forradalmi forrása lehet (atomhurok kristályrácsban), hozzájárulnak a diffúziós folyamatok gyorsulásához. A diszlokációk csökkenthetik az új fázis nukleációjának munkáját, amely a preferenciális kiválasztás területe (például a csapadék keményedése esetén).
Ficam elmélete leírja a kölcsönhatás természetének diszlokációk diszperz részecskék más fázisok és feltárja a oka az öregedés keményíthető.
Tehát a fém tudomány számos kérdése elválaszthatatlanul kapcsolódik a diszlokációk elméletéhez. diszlokáció elmélet kéri a megvalósítása rejtett tartalék erő a fémek, amely abban teljesebb felhasználása az erők atomi kötések a kristályrács. Ez tükröződik, többek között az innovatív, lényegében diszlokáció-mentes anyag - bajuszát fémek és egyéb kristályos anyagok (. Grafit, oxidok, stb), amelynek rendkívül nagy szilárdságú szilárdságának a növeléséhez a korábban ismert típusú acél a kombinált termomechanikai kezelés, (TMT).
A diszlokációelmélet a fém tudomány fejlődését és gyakorlati alkalmazását segíti elő.
2. ellenőrzési feladat
Annak meghatározására, teherbírás N. kN közvetlen szakító tompavarrat két lap 500h25mm részén acélból S275. A varratminőség ellenőrzése - vizuális.
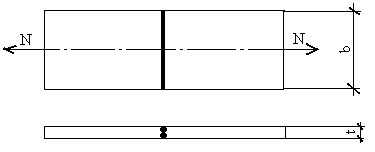
A megoldás. Határozzuk meg az acél és a hegesztett ízületek tervezési ellenállását az 51., / 3 /. Táblázatban szereplő adatok felhasználásával. C275 acéllemez esetében, vastagsága 25 mm, a kialakítás ellenáll a hozampontnak
Ry = 270 MPa (27 kN / cm 2); egy hegesztett tompakötés a húzásra, és a hiányában a fizikai hegesztési minőség-ellenőrzés számított ellenállása 3. táblázat, / 3 /, rwy = 0,85Ry = 0,85 ∙ 270 =
= 229,5 MPa = 22,95 kN / cm 2.
N. teherbírás kN tompavarrat, definiáljuk a feltétele annak biztosítása, az erejét a hegesztett kötések által meghatározott általános képletű (146) / 3 /