Szögek és oldalak háromszögekben, matematika

85. Egy ősáru ΔABC-t (mod 92) alakítunk AB = BC-vel. Aztán tudjuk, hogy a bázison lévő szöge egyenlő, vagyis ∠A = ∠C. Számoljuk ezeket a szögeket, majd ∠1 = ∠2. Most hozzuk létre az új ABC, ABC, stb. Háromszögeket, hogy az AB és a ∠B oldalak változatlanok maradjanak, de a BC oldala növekszik. Ezután az A szögnek növekednie kell (ami nyilvánvaló), és a C szög csökken: látjuk, hogy ∠3 <∠2, ∠4 <∠3 и т. д. потому что ∠2 есть внешний угол для ∆ACC' и, следов. ∠2> ∠3 vagy ∠3 <∠2, также ∠3 есть внешний угол ∆AC'C'' и, след. ∠3> ∠4 vagy ∠4 <∠3 и т. д. (уменьшение угла C видно еще из того, что сумма углов треугольника всегда равна 2d: угол B не изменяется, угол A увеличивается, – след. ∠C должен уменьшаться).

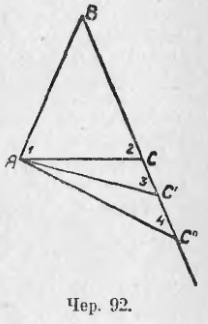
Ezekből a konstrukciókból jogunkban áll következtetéseket levonni:

1) Ha két oldal egyenlő háromszögben, akkor egyenlő szögeket helyeznek el.

2) Ha a két oldal nem egyenlő a háromszögben, akkor a nagyobb szög a nagyobb szemben fekszik.

86. Most, éppen ellenkezőleg, konstruálunk 1) háromszög két egyenlő szögek és 2) háromszög két egyenlőtlen szögek és összehasonlítani az ellentétes oldalon ez a sarok. Az itt felmerülő problémák megoldása érdekében a matematika gyakran alkalmazott érvelésének módját fogjuk használni.

1) Legyen ΔABC (93) állandó legyen, hogy ∠A = ∠C. Hasonlítsa össze a BC és a BA oldalait.

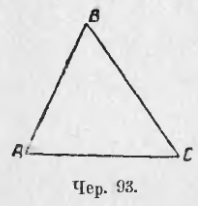
Eddig, anélkül, hogy tudnánk bármit AB és BC oldalairól, 3 feltételezést tudunk tenni róluk: 1) AB = BC, 2) AB> BC és 3) AB A BC-nek az előző alfejezet alapján következménye lehet, hogy ∠C> ∠A, és a következőket hoztuk létre: ∠C = ∠A. Ezért ezt a feltételezést törölni kell. Továbbá a harmadik feltételezésből, hogy az AB ∠C, ami szintén ellentmond a mi konstrukcióinknak. Következésképpen ezt a feltevést is törölni kell. Ezért csak egy feltételezés marad, hogy AB = BC, ami igaznak kell lennie, mivel mások nem hajthatók végre. Ezért van:

Ha két szög egyenlő a háromszögben, akkor egyenlő oldalak fekszenek rájuk.

2) Engedje meg, hogy ΔABC (93) legyen állandó, hogy ∠A> ∠C. Hasonlítsa össze a BA és BC oldalait.
Ismét 3 feltételezést tudunk készíteni: 1) AB = BC, 2) AB> BC és 3) AB A BC nem alkalmas, mivel azt jelenti, hogy ∠C> ∠A, ami ellentmond az építésnek. Csak az a harmadik feltételezés marad, hogy az AB

Ha a háromszög két sarkának egyenlőtlen, akkor a nagyobb oldal a nagyobb szemben áll.

Most a kérdések könnyen megoldhatók: 1) melyik oldalán a jobb szögű háromszög a legnagyobb? 2) A tompaszög háromoldala melyik oldala a legnagyobb?

87. A két előző bekezdésben. két ponttal foglalkozunk: 1) nagyobb szög van a nagyobb oldalon és 2) nagyobb oldal a nagyobb szög ellen. Megállapítottuk, hogy ezek a gondolatok egy háromszögre igazak. Felmerül a kérdés, hogy két háromszögre érvényesek-e. Két egyenlő háromszög esetén kétségtelenül igaz. mivel az egyenlő háromszögek egyetlen szimbólummal egyesíthetők szuperpozícióval. De általánosságban elmondható, hogy két különböző (nem egyenlő) háromszögek, ezek a rendelkezések nem alkalmazhatók: építhetünk két ilyen háromszögek ΔABC és ΔA'B'C „(94 június) volt ∠B> ∠B” , de AC lenne

Ez az eset könnyen érthető vizuálisan. Két AB és BC rúdot (95bis) veszünk fel, és a végét hozzáadjuk (a B pontban). Ha forog a pálcát BC közel az a pont, a B nyíl az ∠B növeli: a BC oldalon meg fog változni a helyzet (akkor is, ha egyikük a BC), de minden alkalommal BC egyenlő marad magára; az AB szegmens szintén nem változik. Vegye figyelembe, hogy az A és C pontok egy másik AC szegmenst definiálnak, amely nem szerepel a rajzon. Amikor a fenti rotációs C pont a helyzetét megváltoztatja, és nyilvánvaló, hogy ez a szegmens AC, nem látható a rajzon, növelni kell (pl. AC „> AC), m. E. Ha a két oldalán a háromszög nem változott, és az a szög közéjük növekszik, akkor a harmadik fél is növekszik. A szövegben ezt az ügyet egy ilyen vizuális reprezentáció nélkül tisztázzák.

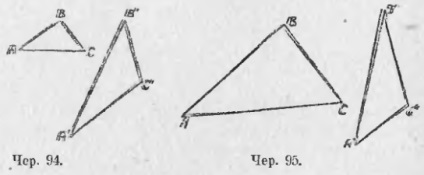
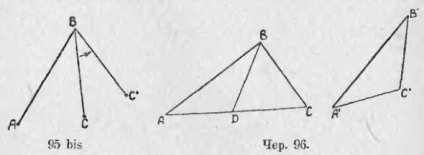
Két ilyen háromszöget építünk fel úgy, hogy két egyenlő oldala van, de a közöttük levő szögek nem egyenlőek. Hagyja ΔABC és ΔA'B'C '(június 95.), van AB = A'B', BC = B'C 'hanem ∠B> ∠B'. Összehasonlítsuk az AC és az A'C 'oldalakat, amelyek egyenlőtlen szögekkel szemben helyezkednek el. Ahhoz, hogy ezt elérjük, szabhat ΔA'B'C „on ΔABC az oldalsó A'B” egyenlő egybeesik az oldalán AB. Ezután a B'C oldalnak be kell mennie ∠B-be, mert ∠B ' <∠B, но где кончится эта сторона, т. е. где расположится точка C', неизвестно. Может быть, она расположится как раз на стороне AC, может быть, расположится вне ∆ABC, а может быть внутри этого треугольника. Разберем эти три случая отдельно.

1) Legyen ΔA'B'C 'legyen elhelyezve úgy, hogy a ΔABD pozícióba (96. ábra) kerüljön, úgyhogy a C' pont D-be, AC oldalra esik; akkor nyilvánvalóan AD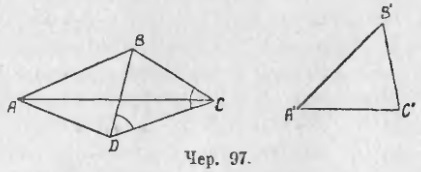

2) Tegyük fel, hogy ΔA'B'C 'feltételezi a ΔABD (fekete 97) pozíciót átfedés esetén, azaz a C' pont a D ponton található, a ΔABC-n kívül. Ezután csatlakoztassa a C és D pontok, fogadása ΔBCD, amely BC = BD, mivel az építési, B'C „= BC, és BD van ugyanazon az oldalon B'C”, csak a másik helyre. Ezért a ΔBCD egyenlő, és ∠BCD = ∠BDC. Tekintsük most a ACAD; körülbelül két sarokban, és ez körülbelül ∠C (vagy ∠ACD) és körülbelül ∠D (vagy ∠ADC) könnyű kitalálni, és jelölt egyenlő szögek egyenlő szárú háromszög, amelyben az egyik nagyobb, mint a másik. Tény, hogy látjuk, hogy ∠ACD <отмеченного угла BCD при основании равнобедренного треугольника, а ∠ADC> jelölt szögű BDC egy egyenlő háromszög alatt. De ∠BCD = ∠BDC, ezért ∠ADC> ∠ACD. . Ezért alapján tétel 86 (azt alkalmazni ΔACD) van AC> AD AD de oldala A'C „át egy másik helyre - így AC> A'C”.

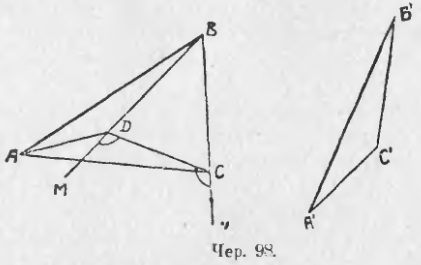
3) Tegyük fel, hogy ΔA'B'C 'a ΔABD (cf 98) pozíciót feltételezi átfedés esetén, vagyis a C' pont a ΔABC-ban van elhelyezve. Ezután, összekötő pont C és D, azt kapjuk, egyenlőszárú ΔCBD (BD = BC, BD oldalsó B'C 'át egy másik helyzetbe, és B'C' = ie építési), és ennek következtében, ∠BCD = ∠BDC . Ha továbbra is a BD és BC oldalán irányokban DM és CN, megkapjuk két külső szöge egyenlő szárú háromszög, és ∠MDC ∠NCD, de ∠MDC = ∠NCD, ezért ∠ADC> ∠ACD, és ezért, a p. 86, van AC> AD, vagy AC> A'C '(AD az A'C' oldala, átirányítva egy másik pozícióra).

Tehát mindhárom esetben kiderült, hogy

azaz ha egy háromszög két oldala megegyezik egy másik háromszög két oldalával, de a közöttük lévő szögek nem egyenlőek, akkor a nagy oldal egy nagy szög ellen helyezkedik el.

88. Elemezzük a fordított kérdést. Legyen épített ΔABC és ΔA'B'C '(jún. 95) úgy, hogy AB = A'B', BC = B'C 'de AC> A'C', t. E. két háromszögnek a két egyenlő oldal, de a harmadik felek nem egyenlőek. Hasonlítsa össze a ∠B és ∠B 'értékeket.
Ugyanazt az érvelést alkalmazzuk, mint a 86. §-ban.

Mindaddig, amíg három feltételezést készítünk a B és B szögekről: 1) ∠B = ∠B ', 2) ∠B> ∠B' és 3) ∠B <∠B'.

Az első feltételezés nem szükséges, mert akkor a háromszög, és az építkezés két egyenlő oldalú és egyenlő szögek között, egyenlő lenne, ezért AC „= A'C”, és ez ellentmond az építkezést. A harmadik feltételezés az, hogy ∠B <∠B' также не годится, так как тогда к этим треугольникам был бы применим результат, найденный в предыдущем п. на основании которого имели бы AC ∠B ", ami igaz legyen. Tehát:

Ha a két oldalán a háromszög egyenlő rendre két fél a másikat, de a harmadik fél által ilyen háromszög nem egyenlő, a párt ellen egyre nagyobb szögben.