Folyékony diszpergáló rendszerek viszkozitása - stadopedia
A reológia a deformáció folyamatainak tudománya és a különböző testek időbeni áramlása. A reológia a mechanikai mechanikai tulajdonságokat vizsgálja a deformáció megnyilvánulásával a külső feszültségek hatása alatt. A kifejezés
deformáció a rendszer pontjai relatív elmozdulását jelenti, amelyben folytonosságát nem sértik. Feszültség. A deformáció oka az erő aránya az alkalmazás területére. A legegyszerűbb deformációs típusok a nyújtás és nyírás. A strukturált rendszerek legteljesebb jellemzését a tangenciális feszültségek hatására létrejövő nyírási deformáció tanulmányozásával nyerjük.
Megkülönböztetni a reverzibilis és a maradék deformációkat.
A terhelés eltávolítása után eltűnő deformációk visszafordíthatónak nevezhetők. és a testeket, amelyek a terhelés eltávolítása után visszafordíthatatlanul helyreállítják az eredeti alakot, elasztikus testnek nevezik.
Deformációk, amelyek nem eltűnnek a terhelés eltávolítása után, maradékként. és azok a testek, amelyek a rugalmas határértéket meghaladó feszültségeken maradt deformációkat mutatnak, műanyagnak nevezik. A reziduális deformáció egyik típusa a folyadékok áramlási jellemzője, amelyben a törzs érték folyamatosan nő állandó feszültség mellett.
Az ideálisan viszkózus testek (ideális folyadékok) reológiai tulajdonságai engedelmeskednek Newton törvényének, és az alábbi egyenlet írja le:
ahol P a nyírófeszültség, Pa; # 951; - folyadék viszkozitás, Pa · s; - a deformáció sebessége (a törzs időbeli változása) vagy a folyadékáramlás sebessége.
A 6.1. Egyenletben az arányossági tényező szerepét a viszkozitás (belső súrlódás) játssza, amely a diszpergált rendszer szerkezetét jellemző legfontosabb tulajdonság. A viszkozitás a vizsgált folyadék reológiai állandója, nem függ a mérés módjától, és meghatározza a folyadék képes ellenállni az áramlásnak. A viszkozitás inverze. az úgynevezett folyékonyság.
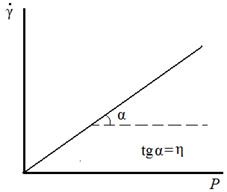
A P-től való függés egyenes, amely a származásból származik. Ennek a vonalnak az abszcissza tengelyre történő lejtőjének érintője határozza meg a viszkozitási értéket, és az y tengely a hozamérték (6.1. Ábra).
A kapillárisból származó ideális folyadékok áramlása érdekében Poiseuille olyan egyenletet javasolt, amely Newton-féle egyenlet különleges esete:
ahol # 951; - a folyadék viszkozitása; P a nyomáskülönbség a kapilláris végén (áramlási nyomás); # 964; - a folyadék kiáramlása a kapillárisból; K a kapilláris állandó (viszkoziméter).
Newton és Poiseuille törvényei szerint a viszkozitás nem függhet a külső nyomástól csak lamináris áramlásban. A turbulencia alatt a viszkozitás növekvő nyomás mellett növekszik, és a viszkózus áramlás alapvető törvényei nem alkalmazhatók.
A diszpergált rendszerek viszkozitása különbözik a diszperziós közeg viszkozitásától az oldószer egy részének diszpergált fázissal való töltése miatt. Ahogy a diszpergált fázis koncentrációja nő, a diszperz rendszer viszkozitása megnő. A diszpergáló rendszer viszkozitása és a diszpergált fázis térfogati frakciója közötti összefüggést az Einstein-egyenlet írja le:
ahol # 951; - a diszperziós rendszer viszkozitása; # 951; 0 - a diszperziós közeg viszkozitása; # 966; - a diszperz fázis térfogati frakciója, a diszperz fázis részecskéinek térfogata és a diszpergált rendszer térfogata () aránya; # 945; - együttható, figyelembe véve a részecskék alakját (gömb alakú részecskék esetén) # 945; = 2,5).
Ahogy a diszpergált fázis részecskék koncentrációja nő, a lineáris függőség # 951; - # 966; a részecskék kölcsönös ütközése esetén sérül, de egy adott koncentrációnál a viszkozitás állandó marad. Hasonló rendszereket, amelyeket Newton, Poiseuille és Einstein egyenletei szabályoznak, normálisnak vagy Ninton-nak neveznek.
A strukturált rendszerek esetében az elméleti függőségtől való eltérés még alacsony koncentrációk esetén is megfigyelhető. Az ilyen rendszerek, amelyek nem engedelmeskednek Newton, Poiseuille és Einstein egyenleteinek, az anomálisnak vagy nem-Newton-nak nevezik.
A szerkezet jelenléte megváltoztatja a folyadék áramlását. Tiszta szerkezet nélküli folyadékok esetében a P és P (1. ábra 1. görbéje) lineáris összefüggése állandó állandó viszkozitásnak megfelelő állandó meredekséggel figyelhető meg.
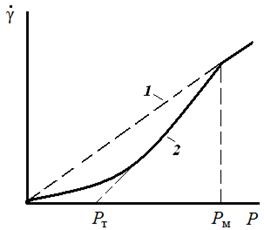
A strukturált rendszereket változó viszkozitású görbék jellemzik, a P függvényében (a 6.2. Ábra szerinti görbe).
Alacsony feszültségnél (p <РТ ) наблюдается медленное течение с малым наклоном. Это течение происходит при максимальной вязкости системы, без разрушения ее структуры, и называется ползучестью .
Ábra. 6.2. A törzsek feszültségének függése Newton-folyadékokra
Ábra. 6.3. Az áramlási sebesség függése a strukturálatlan (1) és strukturált (2) rendszerek feszültségére
Amint a feszültség növekszik, az áramlás sebessége növekszik, ami megfelel a szerkezet elpusztításának. A rendszer viszkozitása csökken, és megfelel a rendszer ún. Műanyag viszkozitásának (). Ebben az esetben a hozamgörbét a Bingham-egyenlet írja le:
hol van a hozampont (a minimális terhelés, amelyen a test elkezd áramlani); - műanyag viszkozitás, amely a szerkezet repedésképességét jellemzi, amikor a terhelés megváltozik.
A hozamterhelés vagy a dinamikus nyíróhatás korlátozása a görbe ezen részének extrapolációja az abszcissza tengelyre, és jellemzi a szerkezet megsemmisítésének megkezdéséhez szükséges erőt. A feszültség további növekedése a szerkezet teljes pusztulását okozza P = PM-ben. A PM értékét a korlátozó nyírófeszültségnek nevezik. Az áramlási görbe utolsó része megfelel a Newton alacsony viszkozitású törvényének.
A non-newtoni folyadékok áramlását leíró általánosabb egyenlet az empirikus Ostwald-Weyl-egyenlet:
ahol k és n empirikus konstansok, amelyek tükrözik az anyag tulajdonságait.
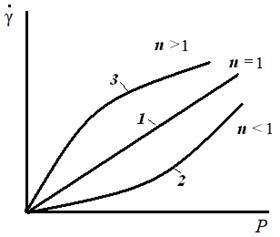
Ábra. 6.4. Áramlási arány
a newtoni feszültségtől (1),
pseudoplasztikus (2) és dilatáns (3) folyadékok
Az n egységességtől való eltérése jellemzi a nem-Newton folyadékok tulajdonságainak eltérését a Newton-folyadékok tulajdonságaitól. Ha n = 1, akkor a folyadék Newtonian, és az állandó k egybeesik a Newton-viszkozitással # 951; N <1 ньютоновская вязкость уменьшается с увеличением скорости сдвига и напряжения. Соответственно этому жидкости называют псевдопластическими . При n> 1 a newton-viszkozitás nő a nyírási sebesség növekedésével. Ennek megfelelően az ilyen folyadékokat dilatánsnak nevezik.
A diszpergáló rendszerek viszkozitásának mérését az áramlási sebességtől függően széles körben alkalmazzák a gyakorlatban. A technológiai folyamatban különböző szakaszaiban a strukturált diszpergáló rendszerek viszkozitása nagymértékben változhat. Bizonyos esetekben például a szállítás során szükséges, hogy a termék maximális viszkozitása legyen, azaz strukturált, és a termék szivattyúzásához ellenkezőleg, olyan minimális viszkozitást kell elérni, amely megfelel a minimális viszkozitásnak.
Az önkontrollhoz kapcsolódó kérdések és feladatok
1. Milyen diszperziós rendszerek strukturális és mechanikai tulajdonságai ismertek?
2. Sorolja fel a szerkezetek típusát.
3. Mi a viszkozitás? Milyen viszkozitást tudsz? Hogyan lehet kvantitatív módon kiszámítani a viszkozitást?
4. Mi határozza meg a diszperziós rendszer viszkozitását?
7. fejezet
OPTIKAI TULAJDONSÁGOK
MEGSZAKÍTNI A RENDSZEREKET
A diszperziós rendszerek optikai tulajdonságai magukban foglalják az abszorpciót, visszaverődést, fénytörést, átvitelet, fényszóródást.
A kolloid kémiai objektumok optikai tulajdonságainak sajátosságait a fő jellemzőik határozzák meg: heterogenitás és diszperzitás. A diszpergáló rendszerek optikai tulajdonságainak vizsgálata a részecskeméret, az alak, a szerkezet és a koncentráció meghatározásának leggyorsabb és legmegfelelőbb eszköze. A kolloid rendszerekre leginkább jellemző a fény felszívódása és szóródása.