Affin transzformációk
Affin transzformációk meghatározása
Beszéljünk a nyújtásról és a lapos formák összenyomásáról.
Ha egy kör mentén húzódsz egy bizonyos irányba, helyi görbét kapsz - ellipszis.
Ha a négyzetet párhuzamos irányban húzza ki, akkor egy téglalapot kap. Ha a négyzetet átlós vonal mentén megnyújtják, vagy benyomják, akkor párhuzamos képet kap.
De mi a nyújtás és a tömörítés? Hogyan határozható meg szigorúan?
A megnyújtás és összehúzódás, amelyekről bizonyos értelemben beszélni fogunk, egységesek.
Ez az egyenletesség azt jelenti, hogy a sík minden darabja ugyanúgy kibővül (zsugorodik).
Ezenkívül, amikor a négyzetet megnyomjuk (összenyomjuk), a szegmensek szegmensek maradnak.
Az ilyen egyenletes kiterjesztéseket (összehúzódásokat) affin transzformációknak nevezzük.
Egy sík átalakítását affine-nek nevezik. ha egyéni, és a vonal bármelyik vonala egy vonal. Az átalakulás egy-egynek mondható. ha eltérő pontokat vesz fel a különböző pontokhoz, és egy pont minden pontra halad.
Emlékezzünk rá, hogy egy átalakítás egy készlet feltérképezése önmagára. A leképezést egy-egy-egynek (bijektívnak) nevezik, ha különböző elemek különbözőekké válnak, és minden egyes elemhez valamilyen elem megy.
Az affin transzformációk egy konkrét esete egyszerűen a mozgások (tömörítés vagy kiterjesztés nélkül). A mozgások olyan átalakulások, amelyek megtartják a távolságot bármely két pont között változatlanul: párhuzamos elválasztások, forgatások, különböző szimmetriák és azok kombinációi.
Az affin transzformációk másik fontos esete a nyújtás és összehúzódás az egyenes vonal tekintetében.
Az 1. ábra a sík különböző mozdulatait mutatja be a rajta lévő házzal. A 2. ábra a sík különböző affin transzformációit mutatja be.
1. ábra. Példák mozgásokra.
2. ábra: affin transzformációk példái.
A sík mozgásának halmazát M o t-nak nevezzük. és az affin átalakítások mint A f f. Ezután a következő állítás igaz.
A mozgások halmaza az affin transzformációk halmazának egy részhalmaza.
Ez nyilvánvalónak tűnik. Értsük meg, mit kell igazolnunk. Ehhez újra meg kell vizsgálnunk a mozgás és az affin transzformációk meghatározását. Szükséges bizonyítani, hogy minden mozgás megegyezik. Ez azt jelenti, hogy meg kell mutatni, hogy a különböző pontok mozgatásakor eltérőek lesznek, és bármelyik vonal képe egyenes vonal.
Intuitíve világos - a mozgás során a számok egyáltalán nem változtatják meg alakjukat és méretüket, de csak a síkon változtatják meg helyzetüket. Továbbá az egyenesek megtartják alakjukat - egyenesen maradnak. Mozgás lehet gondolni, mint mozgó egy darab papírt egy minta az asztalon. Mozgás közben különböző pontok különböznek egymástól, mivel a távolságok megmaradnak. Ha a pontokat "távolítják el" bizonyos távolságra, akkor a mozgás után ugyanolyan távolságban lesznek "osztva".
Meghatározás 3. Egy síknak a k ≠ 0 együtthatójú egyenes vonalához viszonyított kiterjesztése a sík olyan transzformációja, amely alatt minden M pont átmegy egy ilyen M 'pontra. hogy az 1-es egyenestől M '-ig terjedő távolság k-szor nagyobb, mint az M. pontnál. és az M és M 'pontok vetülete az 1 vonalra esik egybe. Ha a k együttható pozitív, akkor az M és M 'pontok az i vonal egyik oldalán helyezkednek el. ha negatív - akkor más.
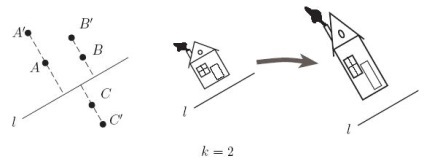
3. ábra. A kompresszió és a nyújtás viszonylag egyenletes.
Bizonyítsuk be, hogy a vonalhoz viszonyított nyúlás (összehúzódás) egy affin transzformáció. Először is ez az átalakulás egy-egy. Ennek bizonyításához megjegyezzük, hogy minden egyes tömörítésnél van egy szakasz, amely minden pont visszatér a helyükre, és fordítva, minden egyes kiterjesztésnél van egy tömörítés, amely mindent visszaad a helyére. És most használjuk a tételt:
Ha az átalakulás g inverz az átalakuláshoz f. és az f transzformáció inverz az átalakuláshoz. g. akkor f és g egy-egy átalakítás.
Az átalakítást g az átalakítás inverzének nevezik f. ha az átalakulás g. az átalakítás után alkalmazzák f. minden pont visszatér a helyükre. Ha az átalakítás f az A pontot áthelyezi a B. pontra. akkor az inverz transzformáció a B pontot az A pontig veszi.
A vonalhoz viszonyított nyújtás (összehúzódás) affin transzformáció.
Továbbra is megmutatjuk, hogy a kontrakció és a kiterjesztés egyenes. Hagyja, hogy a nyújtás az egyenes vonalhoz viszonyítva legyen. Az X tengely mentén haladunk. Vegyünk minden vonalat m. Két lehetséges eset van.
1) Ha metszi a l. akkor az Y tengelyt a metszésponton keresztül húzzuk. X-re merőleges. Ekkor az m vonal egyenlete a következő alakban lesz:
Az m egyenes vonalának pontja (x. Y) = (x A x) a koordinátákkal (x ', y') = (x. K y) = (x, K a x) halad át a pontra. Tehát az új pontok koordinátái megfelelnek az egyenletnek
Egyenes vonal egyenlete. Tehát az y = a x vonal pontjainak képei az y = k a x vonallal vannak.
2) Ha nem metszi l.
Probléma 13.1 [9] Olyan eset, amikor m nem keresztezi az i. kérem, gondoljon magára.
Ha m nem metszi l. akkor minden pontot eltávolítunk az l vonaltól egy bizonyos távolságban d. Az l-vel való összehúzódás vagy nyúj- tás után azok messze távolodnak egyenes vonaltól távol. | k d | és még mindig az egyenes vonal egyik oldalán fekszenek. Így egyenes vonalúak lesznek.
Így a sík mozgások mellett az affin transzformációk kontrakciókat és szakaszokat is tartalmaznak az egyenes vonalhoz képest. Ha a vonalat egy sorra, majd egy másik egyenesre vonatkoztatva alkalmazzuk, akkor ismét affin transzformációt kapunk, hiszen mind az első, mind a második stretching tartotta az egyenes vonalat, és különböző pontokat fordított különböző értékekre. Általánosan igaz
Az affin transzformációk összetétele ismét affin transzformáció:
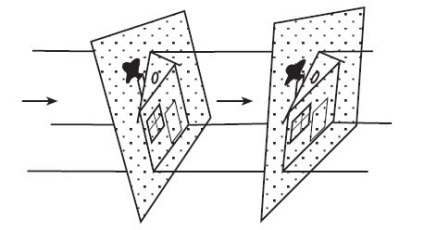
4. ábra. Egy síkban párhuzamos kialakítás esetén az ábrán a sík egyenes metszéspontjához képest megnyújtott (tömörített) alakú.
Bizonyítsuk be, hogy ha egy párhuzamos vetület ábrázol az egyik síkról a másikra, akkor a második a képen
1) egybeesik azzal, ami az első, ha a síkok párhuzamosak;
2) az első síkban ábrázolt, a síkok metszésvonalához viszonyított kiterjesztése (tömörítése), ha a síkok metszi egymást.
Az affin transzformációknak még mindig van egy fontos csoportja - ezek a tömörítés és a kiterjesztés egy pontra vonatkoznak. Ezeket a hasonlóság vagy homotúziák átalakulásának nevezik.