A kínai pontszámokról és a kínai matematikáról, a körülöttem lévő világról
A kínai pontszámokról és a kínai matematikáról
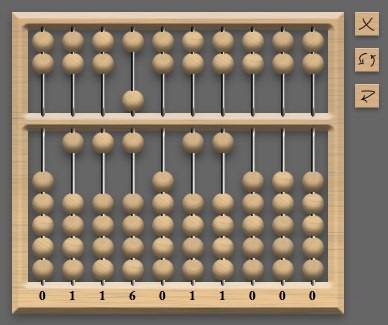
Nem hiszed: a számítások módja a kínai számla segítségével ugyanabban a sorozatban található, mint az iránytű, a papír, a puskapor stb.
A kínaiak bizonyos szakaszban ezt a matematikai módszert nemzeti szinten a tiszteletbeli listán szerepeltették.
Aztán jött az UNESCO-hoz.
By the way, én is megragadta az időt, amikor a bolt-eladók-pénztárosok vigyázni a kötegeket a számlákon.
Bár a pontszámok és a kínaiak hasonlóképpen különböztek.
De mégis: látszólag a pontszámok eltűntek.
Mint általában a számla koncepciója.
Ha a források nem kevernek semmit, az első számok a Kínai Köztársaságra vonatkoznak a 14. századtól az AD-ig.
Henan tartományban találtak.
A 11. században - ismét BC. - a Zhou dinasztia, a matematika és a csillagászat megjelent.
És a matematika tankönyvei is.
Matematika 9 könyvben ...
És nem túlságosan kapcsolatban áll egymással.
A végleges verziót a Zhang Tsan pénzügyi tisztnek tulajdonítják, aki a Kr.e. 150-es évekig elhagyta ezt a halandó világot.
A szerkesztõbizottság 246 feladatot végzett a keleti stílusban: maga a feladat, a válasz és a megoldás módja fogalmazódik meg.
És röviden, és még akkor sem minden esetben.
A feladatokat kereskedőknek, tisztviselőknek, mérnököknek és mérnököknek szánták.
A számokat jelző hieroglifák. megjelent a Kr. e. 2. században.
Végül a III.
Úgy tűnik, azok, akik ma járnak.
Aki Kínába megy, nagyon hasznos tudni.
Legalább, hogy megértsük a kínai árcédulákat.
Azt mondják, hogy a kínai pontszám nagyon hasonlít a miénkhez, az oroszok.
Azok, amelyeket a könyvelõink és a pénztárosaink nem olyan régen használtak.

Matematika az ókori Kínában
Az ősi idők óta nagyon értékes ebben az országban.
Minden tisztviselőnek, hogy megkapja az elszánt széket, kénytelen volt a matematikát a vizsgákon kívül továbbadni.

Korunk korában - 1-5 évszázadban - a kínaiak felfedezik, hogy ilyen arányok, valamint matematikai akciók frakciókkal.
Négyzetes egyenletek és matematikai műveletek negatív számokkal.
Egyébként ezek a számok adósságnak számítottak.
... különböző forrásokban ástak.
Őszintén szólva, magam nem voltam nagyon barátságos az iskolai matematikában, és a szakmám egyáltalán nem matematikai.
Bár tisztelem a matematikát, de most (azaz amikor ásom), sok dolog lenyűgöző.
Például korunk kezdetének időszakában egyfajta (fan-cheng) módszer jelent meg, amely lehetővé tette a tetszőleges lineáris egyenletek számának megoldását.
Később Európában a ma ismert Gauss-módszer került bevezetésre.
Mennyi később - még nem találtam.
És Kínában, ha ismét elhiszik a történelmet, a Tien-jüan módszer (天元 术) bármilyen mértékű egyenlet megoldása nagyon hasonlít a mai Ruffini-Gorner-módszerhez egy polinom gyökereinek megtalálásához.
... Az ókori ókortól kezdve a kínaiok furcsa módon tudták a terület képleteit és a fő alakok és testek kötetét.
És a pitagorai tétel és az algoritmus a pythagorai hármas kiválasztására.
... A 3. század körül Kínában a decimális számok ismertté váltak.
Hamarosan van egy matematikai értekezés a Sun-Tzu - egy kínai matematikus és csillagász.
Életének idejét nem pontosan ismerik - a 3. és 5. század közötti időszakot hívják.
A disszertációban probléma merül fel, amelyen az európai legnagyobb matematikusok sokkal később küszködtek:
találjon olyan számot, amely 3, 5 és 7 részre osztva megadja a maradék 2, 3 és 2 értéket
Azok számára, akik nem értenek sokat erről (mint én), hozzáteszem: az ilyen problémákat gyakran alkalmazzák a naptár elméletében.