Trigonometrikus funkciók, a világtúra enciklopédiája
TRIGONOMETRIKUS FUNKCIÓK
Az egyenlőség geometriai jelentését az 1. ábrán láthatjuk. 11. Itt x az AB ív fele, és sin x a megfelelő akkord fele. Nyilvánvaló, hogy ahogy az A és B pontok egymáshoz közelednek, az akkord hossza pontosabban megközelíti az ív hosszát. Ugyanabból a számból könnyű egyenlőtlenséget kiváltani
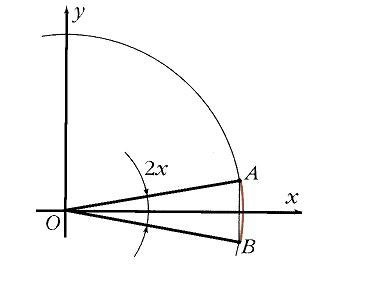
A matematika képletét (*) figyelemre méltó korlátnak nevezik. Ebből különösen az következik, hogy x x kis x-re.
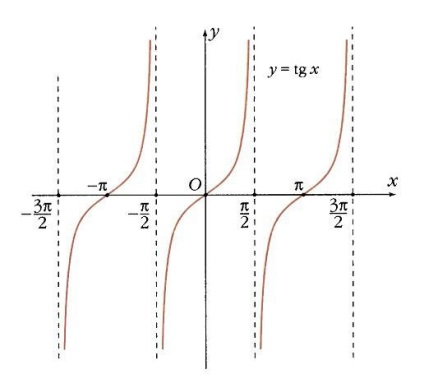
A függvények y = tan x, y = ctg x. Két másik trigonometriai funkciót - a tangent és a cotangent a legegyszerűbben a már ismert szinusz és koszinusz kapcsolatának -
Mint szinusz és koszinusz, a tangens és a cotangens időszakos függvények, de ezek periódusa p. azaz a szinusz és a koszinusz fele mérete. Ennek oka egyértelmű: ha a szinusz és a koszin mindkét jelet megváltoztat, akkor arányuk nem változik.
Mivel az érintő nevezőben egy koszinusz van, az érintő nincs meghatározva olyan pontokon, ahol a koszinusz 0, amikor x = p / 2 + k p. Minden más ponton monoton módon növekszik. Az egyenes vonalak x = p / 2 + k p az érintőhöz függőleges aszimptoták. A k p pontokban az érintő és a lejtés értéke 0 és 1, (12. ábra).
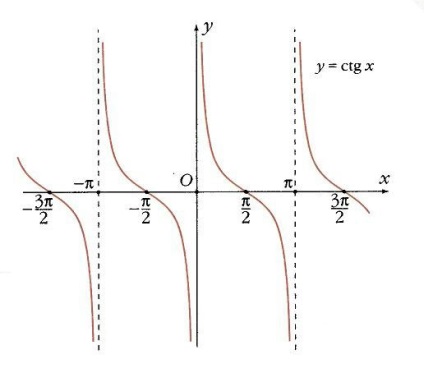
A cotangent nem definiált, ahol a szinusz 0 (ha x = k p). Más pontokon monoton módon csökken, és az x = k p vonalak a függőleges aszimptoták. Az x = p / 2 + k p pontokban a cotangens 0-ra változik, és a szögérték egy ponton -1 (13. ábra).
Paritás és gyakoriság.
Egy függvényt akkor is mondhatunk, ha f (-x) = f (x). A koszinusz és a secant funkciók egyenletesek, a szinusz, a tangens, a cotangens és a koszinusz furcsa funkciók:
sin (-α) = - sin α
tg (-α) = - tan α