Folytonossági módszerek és intervallumok
legfontosabb nbsp> nbsp Wiki bemutató nbsp> nbsp Math nbsp> nbsp10 osztályban nbsp> nbsp Folytonos alkalmazások: intervallum módszer és példák
A függvény folytonosnak mondható az x0 pontnál, ha f (x) f (x0) -ra feszült, miközben x az x0-ig terjed. Továbbá, f (x) - A = f (x) - f (x0) = Δf. Ha az f függvény folytonos minden pontján az intervallum A, ez a funkció folyamatos lesz az egész intervallum A. és azt az időszakot egy, az úgynevezett ebben az esetben egy intervallum folytonosságát az f függvény.
Menetrend folytonos függvények tanult az iskolában természetesen a matematika lehet levonni „anélkül, hogy ceruza, papír”, hiszen ez jelenti a folyamatos vonal. Ha egy bizonyos intervallumban (a; b) az f függvény folyamatos, és nem tűnik el, akkor ebben az intervallumban állandó jel marad.
Ez a tulajdonság nagyon könnyen érthető. Az Ox tengely fölött elhelyezkedő funkció pluszjelet tartalmaz, az Ox tengely alatti funkció mínusz jele. Ha a függvény vonala nem metszi az Ox tengelyt (az Ox tengelyen a funkció nulla), akkor nyilvánvalóan nem változik a jel.
Az intervallumok módja
A függvények folytonossága tulajdonságainak egyik legfényesebb alkalmazása az intervallum módszer, amelyet egy változó egyenlőtlenségeinek megoldására használnak. Tegyük fel, hogy bizonyos funkciók folyamatosak az A intervallumon és eltűnnek az adott intervallum véges számú pontján.
A fenti tulajdonság használatával ezek a pontok megszakítják az A teljes intervallumot olyan intervallumokra, amelyekben a funkció tárolja a jelet. Az összes intervallum jeleinek meghatározásához elegendő megismerni bármelyike közül az egyiket.
Példa egy olyan funkcióra, amely nem folyamatos
Eddig csak folyamatos funkciókat észleltünk. De vannak olyan funkciók, amelyek nem mindig folyamatosak minden olyan pontban, amelyben definiáltak. Például az f (x) = függvény, ahol - az x szám frakcionális része. Grafikáját a következő ábra mutatja.
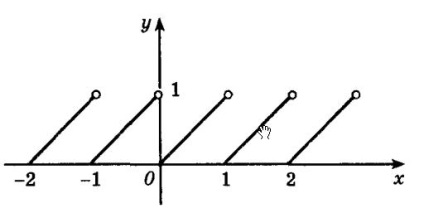
Könnyű látni, hogy egy függvény folytonosságának alapjellemzője egy olyan x0 pontban, amely bármely egész számnak felel meg, nem teljesül. Ugyanakkor az f (x) = függvény folyamatosan minden olyan ponton, amelyen meghatározásra kerül, kivéve olyan pontokon, ahol x egész szám. A grafikonon az ilyen pontok lyukasztott körökkel vannak jelölve.
A funkciók egy adott ponton folyamatosak, de nem különböztethetők meg
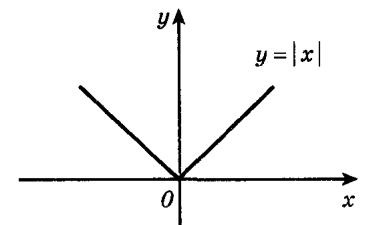
Vannak olyan funkciók, amelyek a definíciók minden pontján folyamatosak. De bizonyos pontokon nem lesz származék. Például a y = | x | függvény folytatódik az egész numerikus tengelyen, de az x = 0 pontban nem különböztethető meg. Az alábbiakban egy grafikon látható ennek a függvénynek.