Az alap helyettesítése 1
A koordináták transzformáció mátrixa
Az E n térben két különálló bázist veszünk fel: e 1, e 2. e n és E 1, E 2. E n
Az indoklást az n = 3 esetre végezzük. Ugyanaz a x-es vektor a különböző bázisokhoz képest különböző koordinátákat tartalmaz. Meg tudjuk írni:
A második bázis bármely vektora az első bázishoz képest bővíthető, azaz
A terjeszkedés egyediségének köszönhetően meg kell állapítanunk az e1, e2, e3 vektorok együtthatóit és az eredményeket. majd
Bemutatunk mátrixokat
Ezután a kapott kapcsolatok X = Z ⋅ X 'mátrix formában írhatók.
A Z mátrixot a régi alapból az új koordináta-transzformációs mátrixnak nevezzük, azaz. az e 1, e 2. és e alapok alapján az E 1, E 2. alapokra. Ezenkívül a koordináta-transzformációs mátrix oszlopai az új E 1, E 2. E n alap vektorának koordinátái az e 1, e 2. e n.
Egy lineáris operátor mátrixának megváltoztatása új alapon történő áttérés esetén
Adjuk meg az A lineáris operátort az E n térben. y = A ⋅ x
Vagy Y = A⋅X. ahol az X (x 1, x 2 x n), és a T Y (y 1, y 2 y n) T mátrix oszlopainak, ábrázoló a koordinátáit a vektorok x és y vonatkozásában bázissal n 1, 2. e e n. A a lineáris A mátrix.
Ugyanazt a helyet választjuk E n egy másik alapból E 1, E 2. E n. Az új alapon az A lineáris operátor mátrixa más. Jelöljük T mátrix az átalakulás koordinátákat, és az X „és Y” - egyoszlopos mátrixot a koordinátáit a vektorok x és y vonatkozásában az új alapokon, azaz
Az általános alakban kapott eredményt helyettesítjük, majd megkapjuk: T ⋅ Y '= A ⋅ T ⋅ X'
Az egyenlőség bal és jobb oldali oldalát balról jobbra, T -1 -vel szorozzuk. kapjuk: Y '= T -1 ⋅ A ⋅ T ∙ X'.
Tehát, ha E n-ben egy új alapra költözünk, akkor a lineáris operátor mátrixa is változik, és a legáltalánosabb esetben egyenlő lesz T -1 ⋅ A ⋅ T.
Egy példa. Az A kezelő az E3 mező alapján
Keresse meg a mátrixát az alapon
Megoldás: Az új alapon az operátor mátrixát a B = T -1 AT képlet adja meg. ahol T az átmenet mátrix a régi alapból az újhoz. Az átmeneti mátrix a T = X -1 ⋅ Y képletből származik.
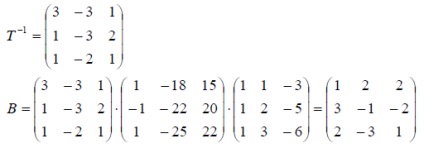
Konjugátum és önműködő operátor
Tegyük fel, hogy egy igazi euklideszi térben E n egy lineáris operátor
1. meghatározás. Operator A * valós euklideszi térben E n nevezzük konjugátum képest a lineáris operátor A ugyanabban a térben, ha a mátrix bármilyen ortonormális alapján a tér nirovannoy ültették mátrix tekintetében üzemeltető A.
A szomszédos üzemeltető tulajdonságai
1. E * = E, ahol E az azonosító operátor, azaz. Az az operátor, akinek az E mátrix az En azonosítója
4. Ha A -1 létezik, akkor (A -1) * = (A *) -1.
2. meghatározás. Az A lineáris operátor egy valós euklideszi térben E n. az úgynevezett selfadjoint. vagy szimmetrikus. Ha küldi az adós A * üzemeltetővel. azaz ha A * = A.
Az önmagával rendelkező operátor mátrixa egyezik az átültetéssel bármely ortonormális alapon, azaz. szimmetrikus a fő átlóval szemben.
Egy önellátó üzemeltető tulajdonságai
1. ha A * = A. B * = B. akkor (A + B) * = A * + B * = A + B;
2. Ha A egy nem degenerált önadszolga operátor, akkor (A -1) * = (A *) -1 = A -1.
Bizonyítás. Valóban, ha létezik A -1, és ezen kívül A * = A. akkor a szomszédos operátor 4 tulajdonsága révén (A -1) * = (A *) -1 = A -1;
3. Ha A egy önhordó operátor az E n valós térben. akkor az egyenlőség tartja:
Sajátvektorok és egy lineáris operátor sajátértékek
Legyen A lineáris operátor. Legyen x∈Ε 1. ahol E 1 az E n tér szubttere. Az y = A x vektor az E 1 szubsztrába tartozhat. Vagy talán nem tartozhat.
Definíció. Az E1 szubsztrát az A. együttműködtető vonatkozásában invariánsnak mondható. ha A x∈ Ε 1. ∀ x∈ Ε 1.
Definíció. Az x nem nulla vektort az A lineáris operátor sajátvektorának nevezzük. Ha van egy λ szám. hogy az A x = λ x egyenlõség teljesül. Ebben az esetben a λ számot az A operátor sajátértékének (sajátértékének) nevezzük. az x vektornak megfelelő. Az A operátor minden sajátértékének halmaza a spektrumának nevezzük.
Tekintsük az A lineáris operátor sajátértékét és sajátvektorát. Az n = 3 esetet tekintjük. Így feltételezzük, hogy bizonyos alapon az A kezelőnek van egy mátrixa
és hagyja, hogy az egyoszlopos mátrix megfeleljen az x vektornak. Ezután a meghatározás szerint
A problémát a mátrix formában írt lineáris homogén egyenletek rendszerének megoldására redukálták. Nyilvánvalóan ez a rendszer egy nemzero megoldást tartalmaz, ha det (A - λE) = 0. A det (A - λE) = 0 egyenletet az A kezelő műveleti egységeinek nevezzük; A det (A - λE) polinomot az A karakterisztikus polinom operátornak nevezik. A koordinátarendszerben a jellemző egyenlet így néz ki:
Megoldva megtaláljuk a lineáris operátor sajátértékét. Ezután az A. mátrix átlóelemeinek összegére, amelyet ez a mátrix trA vagy az A (trA) nyomkövetőjének nyoma hív. a képlet érvényes. Ezenkívül detA = λ 1 λ 2 λ 3.
Miután az A lineáris operátor sajátértékét megtaláltuk, az egyenletre kell helyettesíteni őket, és meg kell találnunk az x (1) sajátvektorokat. x (2). x (3)
Egy példa. Keressük meg egy lineáris operátor sajátértékét és sajátértékét, amelynek mátrixa
A megoldás. Egy sajátvektor definíciójával egy olyan mátrixoszlopot írhatunk, amely megfelel az A lineáris operátor szükséges x-vektorának;
A mátrix formában kapjuk:
A rendszer homogén, ezért végtelen számú megoldást kínál, ha a rendszer meghatározója nulla, azaz a jellemző egyenletünk van:
Megoldva, akkor ilyen sajátértékeket kapunk λ 1 = -1; λ 2 = 3.
Megtaláljuk a megfelelő sajátvektorokat.
1) λ 1 = -1 helyettesítjük a kapott egyenletben
ahol t (1) egy bizonyos paraméter. Így van egy sor kollineáris vektor, amely megfelel az első sajátértéknek: λ 1 = -1:
Ez a vektor könnyen normalizálható, akkor kapunk egy egység sajátvektort, amely megfelel az első sajátértéknek: λ1 = -1,
2) λ 2 = 3 helyettesítjük a kapott egyenletbe
Végezetül, vegye figyelembe, hogy az y = A x vektorok halmaza. ahol x∈ E n. az A lineáris operátor értékének tartománya E n-ben. és az összes x∈E 1 ⊂ E n vektor készletét. hogy az A x = 0, egy lineáris operátor kernele.
Saját adjoint üzemeltető sajátértékek és sajátvektorok tulajdonságai
Az "A" önmegfeleltető operátort az E n valóban euklideszi térben definiáljuk. Mátrixának meghatározásával A szimmetrikus.
ELMÉLET 1. Az A sajátadjához tartozó operátor sajátértékek valós számok.
Tétel 2. A sajátjellegű kezelő két különálló sajátértékének megfelelő sajátvektorok ortogonálisak.
> Bizonyítás. Legyen az A. önadszemélyes operátor különböző sajátérték-értékei, és x 1 x 2 a hozzájuk tartozó sajátértékek. majd
De ez az. az egyenlők bal oldala egyenlő, ezért elvonjuk őket kifejezés szerint, kapjuk: ez azt jelenti, hogy az x 1 x 2 sajátvektorok ortogonálisak.
Megjegyzés. Mivel az A sajátadjához tartozó operátor sajátvektorai ortogonálisak, a lineáris tér alapját képezhetik ennek a lineáris operátornak. Miután az egyes vektorokat hossza alapján osztjuk el, orthonormális alapot kapunk.
Tétel 3. Az önműködő operátor egység sajátvektorai alapján az operátor mátrixa átlós, az átlóelemek pedig sajátértékek.
Bizonyítás. A bizonyíték által az esetben n = 3. Legyen E 1. e 2. e 3 - egység vektorok egy önadjungált A üzemeltető tekintetében a alapján a lineáris tér E 3. megfelelő sajátértékei a lineáris operátor, azaz . Az 1. e 2. e 3 vektorokat egy lineáris tér alapjául vesszük. Nyilvánvaló, hogy ezen a vonalon a vektorok koordinátái vannak:
. Következésképpen az A operátor A mátrixa az e 1. e 2. e 3 alapban az alábbi alakú:
Az ilyen alap kiválasztása, amelyben egy lineáris operátor mátrixa átlós formában van, a mátrix redukciója az átlós alaknak nevezik.