Számozott számok
ÁBRA SZÁMOK
A Pro számok 25, 49, 100 négyzetek. És miért? Mert akkor kapjuk, ha a buildszámot 5, 7 és 10 a téren. De függetlenül attól, hogy a neve bármilyen kapcsolatban az a geometriai formák - szögletes? Nézzük Fig. 1. A katonák vannak szabályos sorokban, alkotó négyzetek. A katonák számát, a téren könnyen kiszámítható - szükség van, hogy szaporodnak a számot a vízszintes oldalán katonák számát a függőleges oldala (vegye figyelembe, hogy ezek a számok azonos), és kapsz az összes katonát a téren.

Az ősi időkben a kalkulátorokat gyakran kavicsokkal számolták, és természetesen vannak olyan esetek, amikor a kövek rendszeresen alakulnak át. A négyzetszámok mellett háromszög alakú számokat is ismertek, amelyeket a 2. ábrán látható módon kaptunk. 2 a felső részen. Nem nehéz megérteni, hogy a negyedik szám egyenlő, és a harmadik háromszög azonos az összes 1-es egész szám összegével, (lásd A számtani előrehaladás).
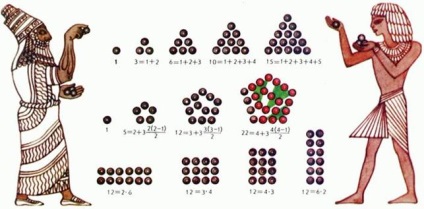
Az ötszögű számok a 3. ábrán láthatók. 2. Az ötödik ötszög számának megadásához három háromszög alakú számot kell osztani, amelyek után még vannak pontok, amint az az ábrán látható. Ennek eredményeképpen megkapjuk, hogy a második ötszög.
Hasonlóképpen bármely poligonszámot is létrehozhat. Az n-szögszámú képlet a következő:
Amikor háromszög alakú számokat kapunk, négyzetekkel stb.
Hasonlóképpen számot is megjeleníthet egy négyszög formájában. A 12-es számnál ez sokféleképpen történhet (2. ábra), a 13-as szám pedig csak egy sorba helyezi az elemeket. Egy ilyen ősi szám nem tekinthető téglalap alakúnak. Így a négyszögletes számok mind összetett számok, és a nem téglalap alakú számok a prímszámok.
Az ábrás számok tartalmazzák a piramis alakú számokat is, amelyeket akkor kapnak, ha a golyókat egy piramisban összegyűjtik, mint ahogyan az ágyú körül lévő magok összecsukva voltak. Nem nehéz megérteni, hogy a -th. Piramisse szám egyenlő az összes háromszög számmal - az elsőtől a -th. A második piramisse szám kiszámításának formája az űrlap