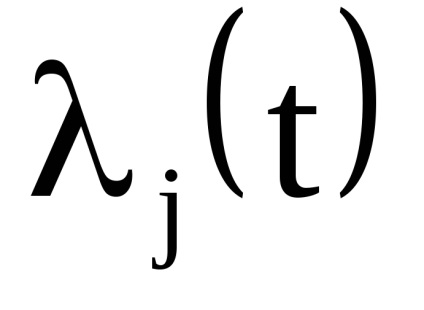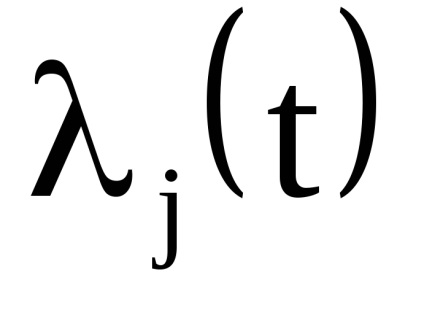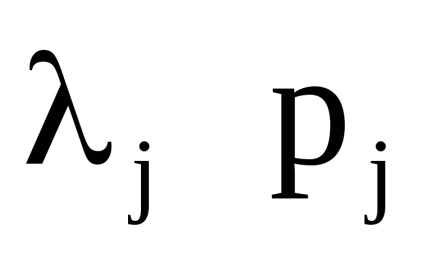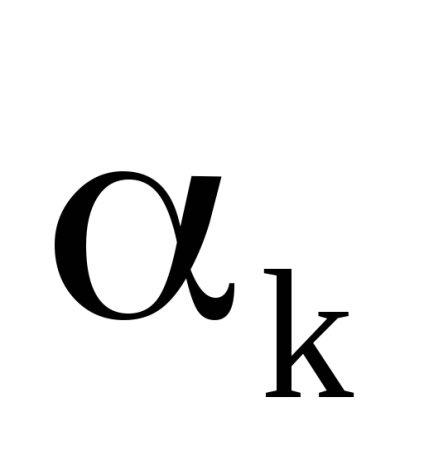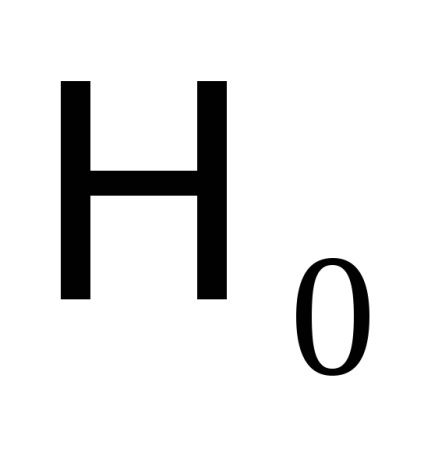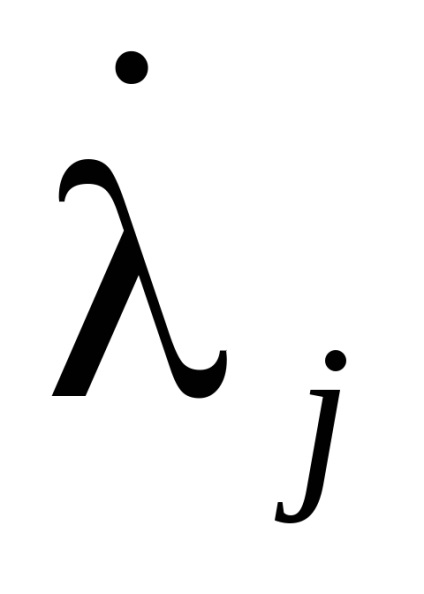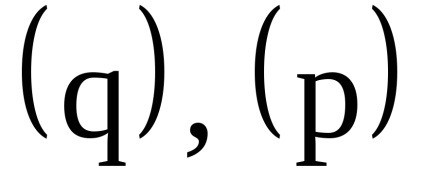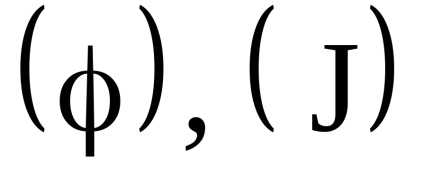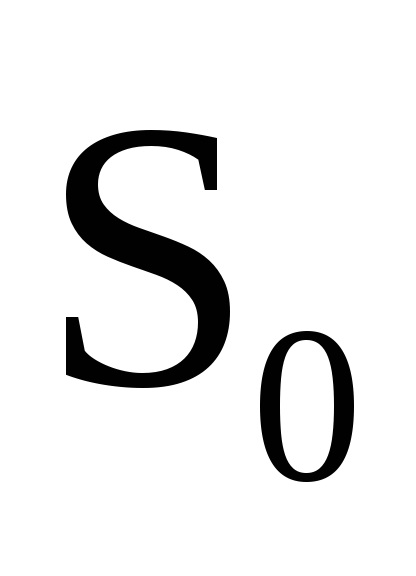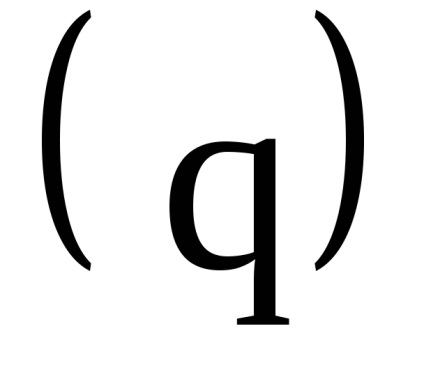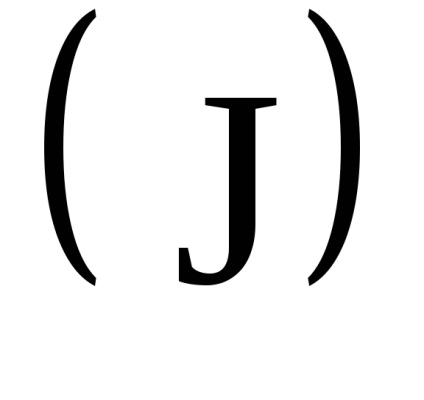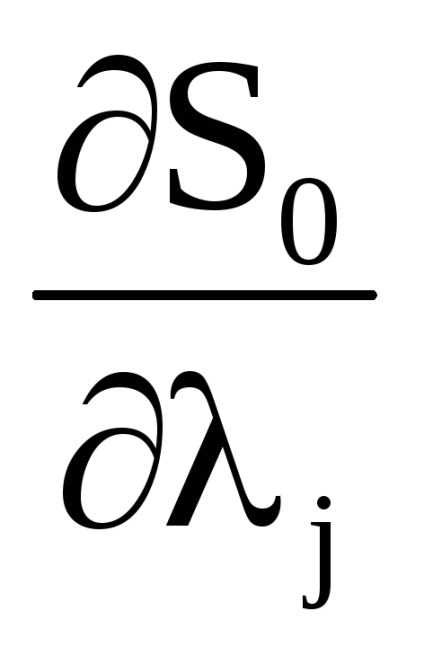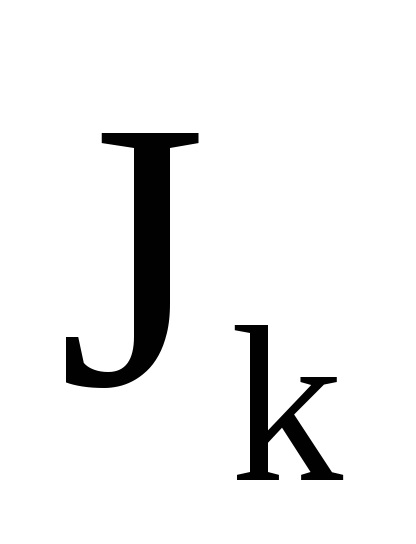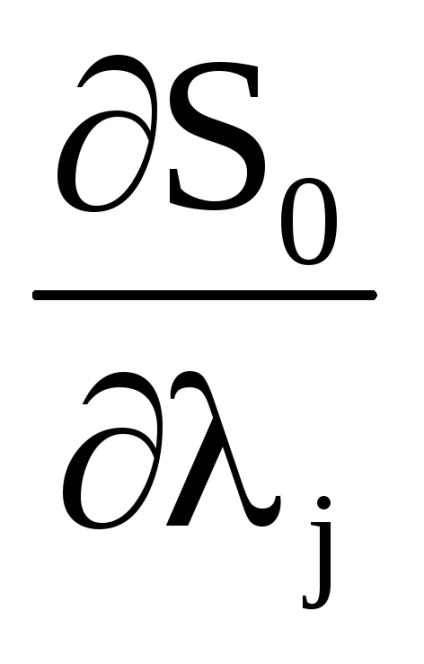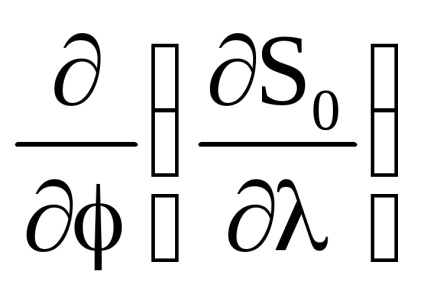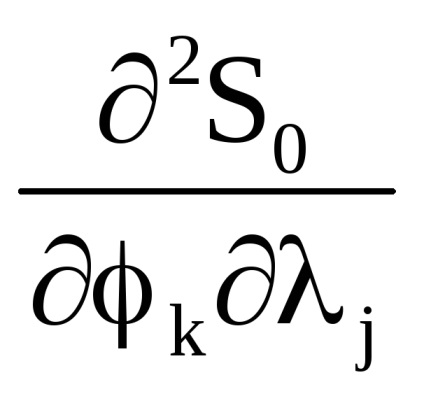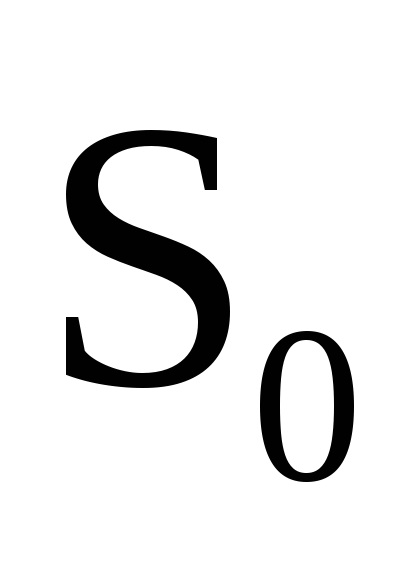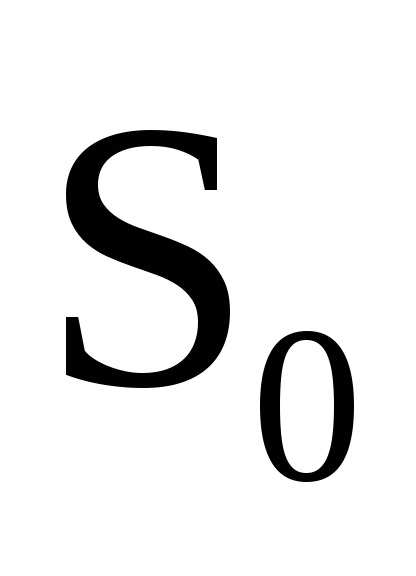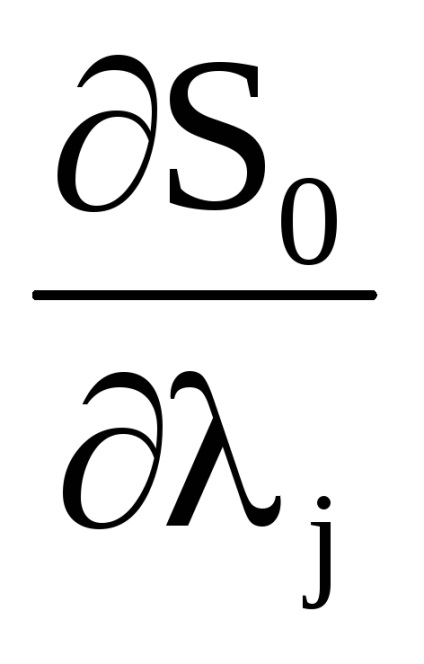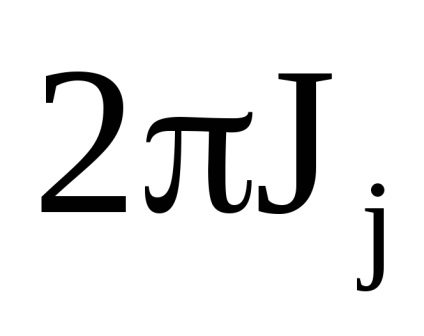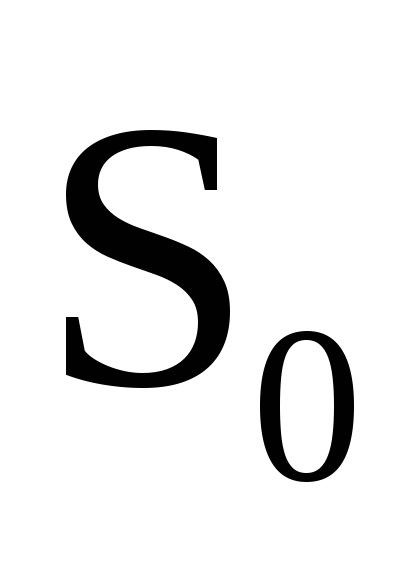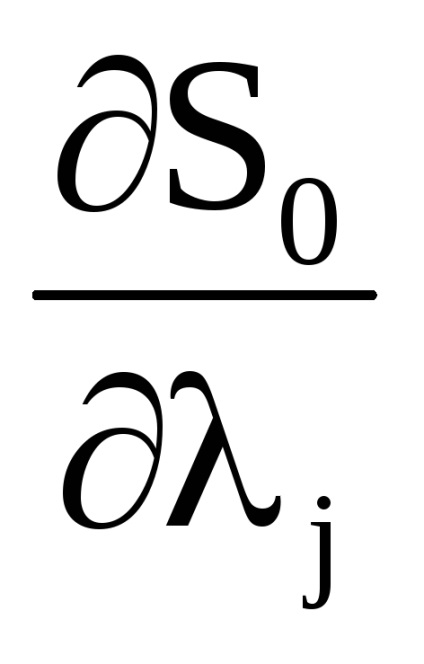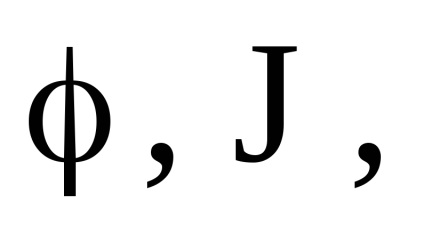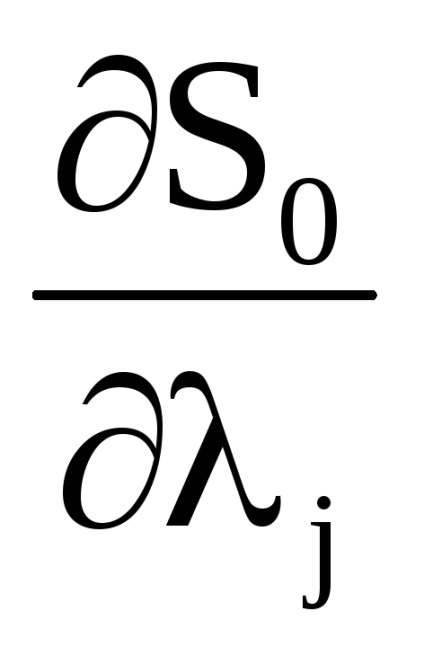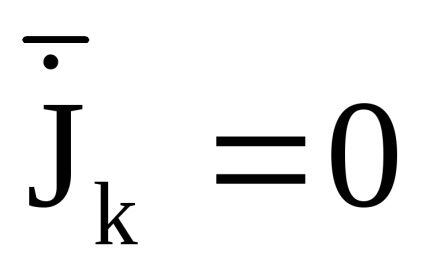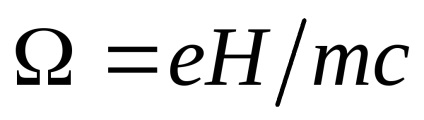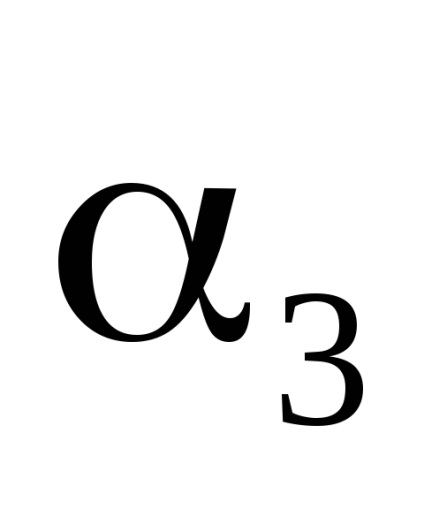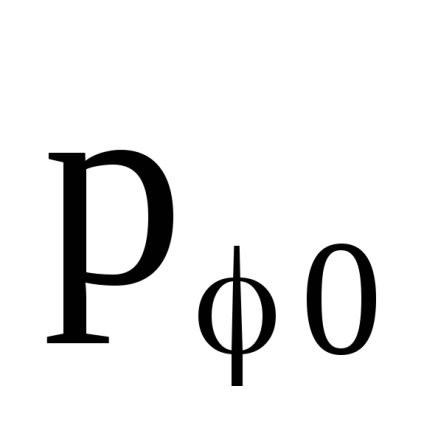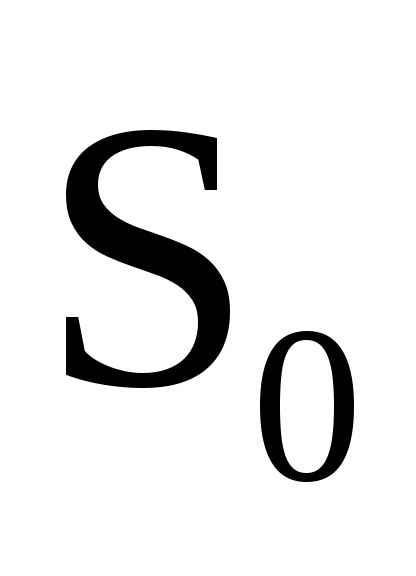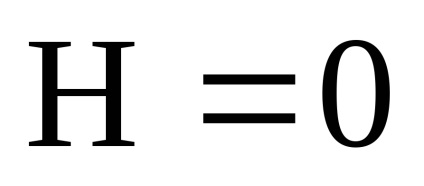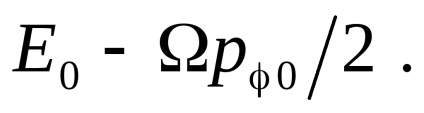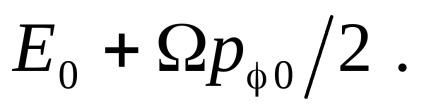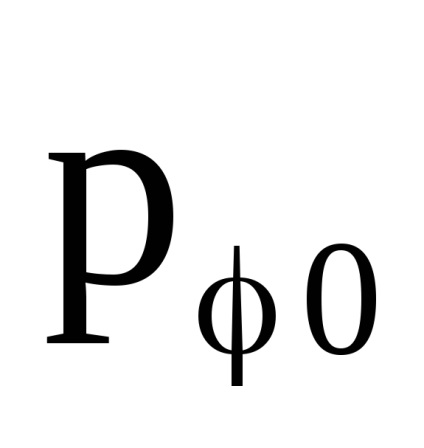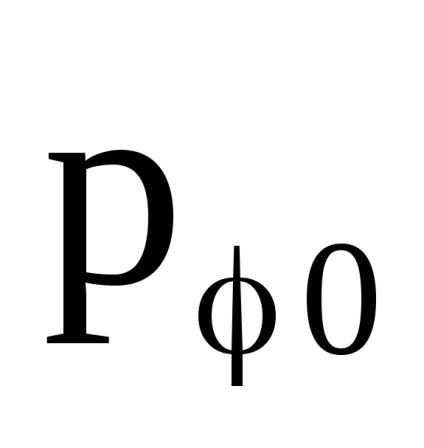Az akcióváltozók egyik fontos tulajdonsága az adiabatikus invariancia tulajdonsága, amely abból áll, hogy az akcióváltozók állandó értéküket is megőrzik azokban az esetekben is, amikor a rendszer hamiltonai az időtől bizonyos paramétereken
, amint azt mondják, adiabatikusan változik az idővel, vagyis nagyon lassan. Lassan értjük azokat a változásokat, amelyek alapján
kis változás időszakonként, egyenlő nagyságrendben az időszakokhoz képest
, azaz,
Nyilvánvaló, hogy az ilyen mechanikus rendszerek nem szigorúan elszigeteltek. Megmutatjuk, hogy az ilyen rendszerekben az akcióváltozók adiabatikus invariánsok.
Tekintsünk egy olyan rendszert, amely minden egyes alkalommal egybeesik a fent vizsgált konzervatív rendszerrel, ami lehetővé teszi a változók teljes szétválasztását. Azt is feltételezzük, hogy a rendszer mozgása véges. Egy ilyen rendszer hamiltonja nyilvánvalóan a paraméterektől függ
, amelyek megfelelnek a feltételeknek (61.11); a formában megjeleníthető
Állandóan
a megfelelő koordináták periodikus funkciói
;
ebben az esetben az idő periódikus függvényei.
Ha a paraméterek
lassan változik idővel, akkor, annak ellenére, hogy a Hamiltonianus (62.11) által leírt rendszer nem konzervatív, a Hamilton-Jacobi egyenlet megoldását a (24.11) -hoz közeli formában lehet keresni:
ahol azonban a paramétereket
, és ezáltal a mennyiségek
és
lassan változik idővel. A (63.11) helyettesítve a Hamilton-Jacobi egyenletbe és figyelmen kívül hagyva ezzel arányosan
, megkapjuk a "zeroth approximation" egyenletét,
A (61.11) szerint ezt az egyenletet úgy lehet megoldani, hogy mindegyiket feltételezzük
állandóak, és csak a felépített megoldásokban tekinthetők idő függvénynek. Ezért a konzervatív rendszerhez kapott összes fenti formula marad érvényben, de az összes kapcsolat most tartalmaz időfüggő paramétereket
.
A változókból származó kanonikus transzformáció generáló funkciója
változókra
függvény függvénye
, amely azonban most attól függ
:
Megjegyezzük
szintén függ
.
A függvény által létrehozott kanonikus transzformáció képletét (65.11) írjuk:
A mozgás új egyenleteinek formája van
Minden képletben a differenciálódás a
Ezt állandóan kell elvégezni
és
; a differenciálódás után a (67.11) szubsztitúció és a (69.11), (70.11)
kifejezést fejezzük ki.
A változók adiabatikus invarianciájának tulajdonságainak bizonyítása
Átlagos egyenleteket (70.11) egy olyan időintervallumon belül, amely kicsi a paraméterek észrevehető változásának idejéhez képest
és elég nagy a rendszer periódusaival összehasonlítva. Az ilyen időintervallum választékával,
(a lassú változás miatt
) ki lehet venni a középső jel alatt. ezért
Most bemutatjuk, hogy a származékok
egyértékű időszakos funkciók
. Ha ez így van, akkor fel lehet bontani Fourier-sorozatra, amelynek együtthatói függenek
és
. Ez viszont a Fourier sorozat a származékok
nem tartalmaz konstans feltételeket, és ezért ha elég nagy időintervallumot kell átlagolni, az összes származékot
Az összes adiabatikus invariancia
bizonyítani fogják.
Megjegyezzük
- a koordináták kétértelmű funkciója
, mivel a (66.11) szerint a formában megjeleníthető
A koordináták megváltoztatásának teljes időtartamára
(a fennmaradó rögzített)
növekszik
funkciók
- a koordináták egyértékű függvényei, mivel különbséget tesznek a
adalékok, többszörösek
, amelyek kétértelműséghez vezetnek
, eltűnik. mert
- egyértékű koordináták funkciói
, akkor ezek a szögváltozók periodikus függvényei
; ezek a funkciók változáskor nem változtatják meg értéküket
a
(adott értékek esetén
). Más szóval, minden egyértékű függvény
, kanonikus változókban kifejezve
mindegyik periodikus függvénye
egy időtartammal
. Tehát minden
egyértékű időszakos funkciók
. Megmutattuk, hogy ebben az esetben minden
és ennélfogva mindent
Az összes cselekvési változó adiabatikus invariancia tulajdonsága bizonyított.
Egy példa. Hogyan változik meg a m tömegű töltött részecske energiája az U (r) középső mezőben, amikor a gyenge homogén mágneses tér H lassan bekapcsolódik?
A töltés Hamilton-függvényét gömb alakú koordinátarendszerben írjuk (a Descartes-koordináta-rendszer Oz tengelye párhuzamos a H-val):
itt
- fénysebesség. A probléma állapota miatt a mágneses mező gyenge, ezért a legutolsó kifejezés (H-beli képpontos) elhanyagolható.
A Hamilton-Jacobi egyenlet figyelembe veszi ezt
ahol
- részecske energia,
-ciklotron frekvencia.
Az oldatot formában keressük
Itt, mint állandó
mi választottuk
. Behelyettesítve
in (74.11), akkor megkapjuk
Az egyenlet (75.11) meghatározza a művelet változó kiszámításához szükséges funkciót
:
nyilván,
egybe fog esni
, számított az ügyben
, ha az utolsó kifejezésben ahelyett, hogy
helyettesíti a kombinációt
Ezért a mennyiség
állandó marad, ha a homogén mágneses mező lassan be van kapcsolva. Ezenkívül a mennyiség
- az általánosított töltési lendület komponense. A fizikai jelentés szerint
- A töltés szögletes impulzusának konzervált vetülete a H vektoron.
Kapcsolódó cikkek