A test merevségének dimenzióinak függőségének vizsgálata
A munka címe: A test merevségének dimenzióinak függése
Szakirány: Fizika
Leírás: A munka célja: a rugalmas erő függőségét az abszolút megnyújtáson keresztül kiszámítja a különböző hosszúságú rugók merevségét. Ezért a rugalmas erők elektromágneses jellegűek. A rugalmasság ereje mindig az egyensúlyi helyzet felé irányul, és hajlamos visszatérni a test eredeti állapotára.
Fájlméret: 176 KB
A munkát letöltötték: 3 fő.
Laboratóriumi mű száma 1.
A test merevségének dimenziójából való függőségének vizsgálata.
A munka célja: a rugalmas erő függőségének az abszolút nyúlás függvényében kiszámítja a különböző hosszúságú rugók merevségét.
Berendezés: állvány, vonalzó, rugó, súlya 100 g.
Elmélet. A deformáció a test térfogatának vagy alakjának megváltoztatását jelenti a külső erők hatása alatt. Ha egy anyag (atomok, molekulák, ionok) közötti részecskék közötti távolság megváltozik, az egymás közötti kölcsönhatás változik. Ahogy a távolság nő, a vonzalom ereje nő és csökken # 150; visszataszító erők. akik megpróbálják visszaadni a test eredeti állapotát. Ezért a rugalmas erők elektromágneses jellegűek. A rugalmasság ereje mindig az egyensúlyi helyzet felé irányul, és hajlamos visszatérni a test eredeti állapotára. A rugalmasság ereje közvetlenül arányos a test abszolút nyúlásával.
Hooke-törvény: A rugalmas erő deformációja során keletkező a test egyenesen arányos a nyúlás (összehúzódás), és ellentétes irányú a részecskék mozgását a test alatt a deformáció. x = Δ l a test kiterjesztése, k # 150; merevségi együttható [k] = N / m. A merevségi együttható a test alakjától és méretétől, valamint az anyagtól függ. Numerikusan megegyezik a test nyúlási (tömörítési) rugalmasságával 1 m-rel.
Az F x rugalmas erő vetületének függése a test megnyúlásánál.
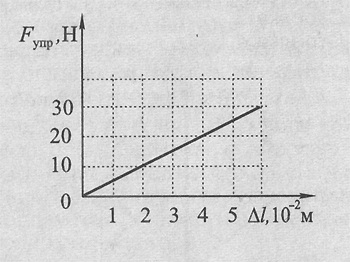
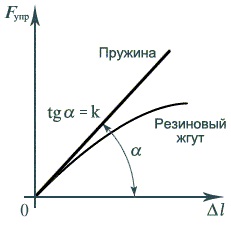
A gráfról világos, hogy tgα = k. Ezzel a formulával meghatározza a test merevségét ebben a laboratóriumi munkában.
A munka sorrendje.
1.Fix a rugó az állvány a fele.
2. Mérje meg a rugó kezdeti hosszát az 1 0 vonalzóval.
3. A rakományt 100 g tömeggel szállítsa.
4. Mérje meg a deformált rugó hosszát l.
5. Számolja ki a rugó hosszabbítóját x 1 = Δ l = l # 150; l 0.
6. A rugó rugóján két teher van
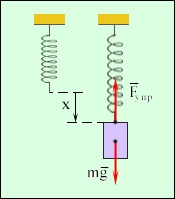
kompenzáló erők: gravitáció és rugalmasság
7. Számítsa ki a rugalmas erőt a képlet segítségével. g = 9,8 m / s 2 - a szabad esés gyorsulása
8. Függessze fel a 200 g súlyú rakományt, és ismételje meg a kísérletet a 4-6. Pontban.
9. Az eredményeket jegyezze fel a táblázatban.
10. Válassza ki a koordináta-rendszert, és ábrázolja a rugalmas F erőnyúlás függését a rugó nyúlásával szemben.
11. Mérje meg a szögmérővel az egyenes és az abszcissza közötti szöget.
12. A táblázatban keresse meg a szög érintőjét.
13. Az 1-es merevség értékére vonatkozó következtetés levonása és az eredmény a táblázatban való rögzítése.
14.Tömítse a rugót az állványba teljes hosszában, és ismételje meg a tesztet a 4-13. Pontokon.
15. Hasonlítsuk össze a k 1 és k 2 értékeket.
16. Határozzuk meg a merevség függését a rugó paraméterein.
A kérdésekre.
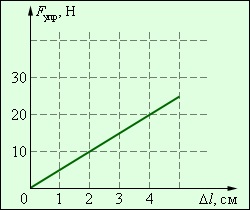
1. Az ábrán a rugalmassági modulus függése a rugó nyúlásával függ össze. Hooke törvénye szerint határozza meg a rugó merevségét.
Adja meg a vonal és az abszcissza közötti szög érintő tangensének fizikai jelentését, a háromszög területét az OA gráf alatt.
2. A 200 H \ m merevség rugóját 2 egyenlő részre vágtuk. Mi az egyes rugók merevsége.
3. Határozza meg a rugó rugalmas erejének, a gravitációs erő és a teher súlyának alkalmazási helyeit.
4. Nevezze meg a rugó rugalmasságának jellegét, a gravitációs erőt és a terhelés súlyát.
5. Oldja meg a problémát. A rugó 4 mm-rel történő nyújtásához 0.02J-os feladatot kell elvégeznie. Milyen munkát kell tennie a tavasz 4 cm-es nyúlásával?