A közlekedési probléma megoldásának egyik példája a ms excel használata
Példa egy közlekedési probléma megoldására MS Excel alkalmazással
A közlekedési probléma a műveletek kivizsgálásának klasszikus feladata. Az erőforrás-allokáció számos feladata lecsökken erre a feladatra.
A gazdaságban öt ásványi trágya raktár van, és négy pontot kell szállítani. Az ásványi műtrágyák minden egyes elemének szükségessége változik, és az egyes raktárakban lévő készletek korlátozottak. Meg kell határoznia, hogy melyik raktárig, ahová szállítandó, mennyi ásványi műtrágya van a teherforgalom minimalizálása érdekében.
A következő kezdeti adatok állnak rendelkezésre.
Ásványi műtrágyák elérhetősége raktárakban.
A konkrét szállítási pont oszlopának metszéspontjában a raktárvonal információi a szállítási pont és a raktár közötti távolságokról. Például a 3 pont és a 3 raktár közötti távolság 10 kilométer.
A probléma megoldásához előkészítjük a szükséges táblázatokat. (1. ábra)
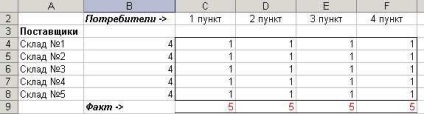
Fig.1 Modifikálható sejtek.
A negyedik és nyolcadik sorban a B oszlopban levő cellák értékeit a C oszlopból az F. oszlophoz tartozó megfelelő sorok sejtjeinek összegzésével határozzuk meg.
Például a B4 = SUM (C4: F4)
A C-F oszlopok 9-es sorában lévő cellák értékeit úgy határozzuk meg, hogy a megfelelő oszlopok cellaadatait összegezzük 4-től 8 sorig.
Például a C9 = SUM (C4: C8)
Az egyes szállítási pontok oszlopának metszéspontjában lévő cellákban lévő összes érték és a raktári vonal az e raktárból származó fogyasztott tonna mennyiségét jelenti a fogyasztási pontig. Az alsó sor (9. sor) összegzi az egyes szállítási pontokhoz szállított ásványi műtrágyák teljes mennyiségét, a második oszlop (B oszlop) összegzi az adott raktárból származó ásványi műtrágyák mennyiségét.
Most, a kiindulási adatok felhasználásával ugyanazon a lapon írjuk be a szükséges mennyiségű készletet, valamint a raktárak és a szállítási pontok közötti távolságokat.
2. ábra Háttérinformációk.
A C-F oszlopokban a 16. sorban minden szállítási pontra meghatározzuk a forgalmat. Például 1 pontra (C16 cella) ez a képlet segítségével számítható ki
С16 = С4 * С1 1 + С5 * С1 2 + С6 * С1 3 + С7 * С14 + С8 * С15
vagy használja a SUMPRODUCT funkciót
A Cell C4 az ásványi műtrágyák mennyiségét tartalmazza az 1-től 1-ig terjedő raktárba szállított szállítási pontoktól, és a C11 cella az 1-től 1-ig terjedő szállítási ponttól való távolság. Ennek megfelelően a képletben szereplő első kifejezés a teljes áruszállítási forgalmat jelenti ezen az útvonalon. Az egész képlet kiszámítja az ásványi műtrágya szállításának teljes szállítási forgalmát 1 szállítási helyen.
A B16 cellában, a képlet = SUM (C16: F16) alkalmazásával kiszámítjuk az ásványi műtrágyák áruszállításának teljes mennyiségét.
Így a munkalapon szereplő információk a következő formában (3. ábra)

Ábra. 3. A szállítási feladat megoldására készített munkalap
A szállítási probléma megoldásához a Keresés megoldás eljárást használjuk, amely az Eszközök menüben található.
A parancs kiválasztása után megjelenik egy párbeszédablak (4. ábra).
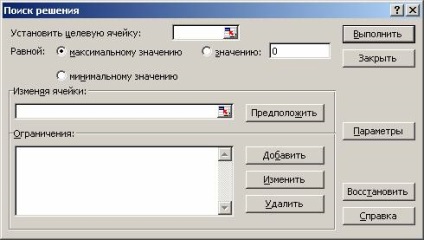
Ábra. 4. A Megoldás keresése párbeszédpanel
Mivel, mint a mi optimalizálási feltétel szerint van megválasztva, hogy minimálisra csökkentsék a forgalom a területen, hogy állítsa be egy célsejtbe, adja meg a referencia a sejt, amely tartalmazza a képlet a térfogatának kiszámításához a forgalom bschego műtrágyák. Ebben az esetben a cella $ B $ 1 6. Annak érdekében, hogy az érték az utolsó cella által megadott értékek befolyása sejtek (érintő, ebben az esetben, és a változó olyan sejtek, amelyek a boltban szükséges értékeket ismeretlen), a kapcsoló a minimális érték;
A Cégek módosítása mezőbe írja be a módosítandó cellákra vonatkozó utalásokat vesszővel elválasztva; vagy ha a sejtek a közelben vannak, jelezve az első és az utolsó cellát, kettősponttal elválasztva ($ C $ 4: $ F $ 8). Ez azt jelenti, hogy a minimális áruszállítás elérése érdekében a C4-F8 cellákban lévő értékek változni fognak. azaz az adott útvonalon szállított rakomány mennyisége megváltozik.
Ha most elkezdjük a paraméterek kiválasztását, találunk egy változatot, ahol minden változó nulla. És ez helyes - ha nem szállít semmit, akkor ez a legolcsóbb lehetőség. De ásványi műtrágyákat kell szállítanunk, ezért bizonyos korlátokat kell meghoznunk ahhoz, hogy megoldást találjunk.
A mezők Limits csoportjában kattintson a Hozzáadás gombra. Megjelenik a Hozzáadás korlátozása párbeszédpanel (5. ábra)
Ábra. 5. A Kényszer hozzáadása párbeszédpanel
A bal oldali margóban meg kell határoznia a kényszer bal oldalát, kiválasztja az értéken feltüntetett feltétel jeleit, és írja be a kényszer jobb oldalát. Mint más esetekben, nem adhat meg linkeket a cellákhoz, de az egérrel válassza ki ezeket a cellákat. Egy korlátozás megadását követően kattintson a Hozzáadás gombra, és írja be a következőket. Ha befejezte az összes korlátozás beírását, kattintson az OK gombra. A párbeszédablakban bevezetik a korlátozások sorát (6. ábra)
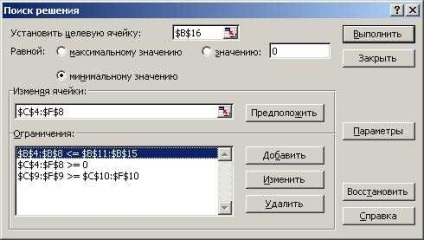
Ábra. 6. A Megoldás megkeresése párbeszédpanel kitöltett mezőkkel
A Megoldáskeresés párbeszédpanel Korlátok listájában lévő korlátozások módosításához és eltávolításához adja meg a módosítani kívánt vagy törölni kívánt korlátozást. Válassza a Módosítások lehetőséget, és hajtsa végre a módosításokat, vagy kattintson az Eltávolítás gombra.
Nézzük meg részletesebben azokat a feltételeket, amelyeket egyes cellákban meg kell határozni a probléma helyes megoldásához.
Az első feltétel $ B $ 4: $ B $ 8 <=$B$11:$B$12. Оно означает, что значение в ячейке В4 должно быть меньше или равно значению в В11. в В5 меньше или равно, чем в В12. и так далее до В8 и В15.
A lapokon a B4-B8 cellákban az egyes raktárakból származó készletek mennyisége található. A B11-B15 sejtekben - ugyanazon raktárakban lévő készletek. Mivel nem lehet többet kivonni a raktárból, mint az, az első érték nem lehet nagyobb a másodiknál.
A második feltétel $ C $ 4: $ F $ 8> = 0. Ez azt jelenti, hogy a forgalom nagysága nem lehet negatív, vagyis ha nincsenek ásványi műtrágyák a raktárban, akkor azokat nem a szállítási ponttól vették át, amelyre az ásványi műtrágyákat korábban importálták. A rakományforgalomnak csak egy iránya van - a raktáraktól a műtrágyaszállításig.
Végül a harmadik és az utolsó feltétel $ C $ 9: $ F $ 9 = $ C $ 10: $ F $ 10. Ez azt jelenti, hogy a kilencedik vonal celláiban lévő értékeknek nagyobbnak vagy egyenlőeknek kell lenniük a tizedik vonal sejtjeinek értékében. vagyis az ásványi műtrágyák szállítási pontjai iránti kérelmeket teljes körűen végre kell hajtani. Az ellátás mennyiségének túlszívása megengedett, és az alulteljesítés nem lehetséges.
A bevezetett feltételeknek lehetővé kell tenni számunkra, hogy megtaláljuk a probléma legoptimálisabb megoldását. A megoldás kiválasztásához kattintson a Futtatás gombra.
Miután megtalálta a megoldást, megjelenik a Solution Solution Results párbeszédablak (7. ábra)
Ábra. 7. Megoldás keresése párbeszédpanel
Az OK gombra kattintva a megoldást a munkalapra visszük (7. ábra).
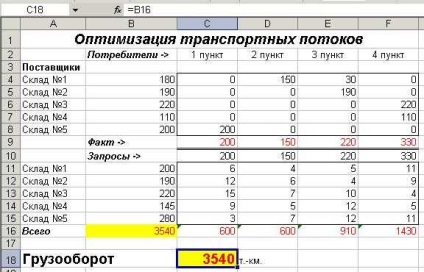
Ábra. 7. A megoldott szállítási probléma
A szállítmányok minimális áruszállítási forgalma az összes feltételnek megfelelően 3540 t.km.