AC áram
A keret, amely 100 fordulat és egyenletesen-Vera-forgó egységes mágneses mező, a mágneses indukció fluxus változások a törvény szerint F = 2,0 * 10 -3 cos 314t [Wb]. Határozza meg: az emf függőségét a keretben. stb. időről időre; az e. stb .; pillanatnyi értéke e. stb. t = 0,0050 s esetén. Hogyan függ majd az e. stb. attól az időponttól kezdve, amikor a keret forgási szögsebessége megduplázódik?
Tekintettel: N = 100 - a keretek fordulatszámát; F = 2,0 * 10 -3 cos314t [Wb] - a függőség a mágneses fluxus az időkeretet, t = 0,0050 s - időt, amely a meghatározott pillanatnyi értéke az EMF
Keresse meg: e = f (t) az emf függvénye a keretben. stb. időről időre; Ԑ0 az e maximális értéke. stb .; Ԑ az e tényleges értéke. stb .; e a pillanatnyi érték e. stb. t = 0,0050 s; e1 = f (t) az e függvénye. stb. attól az időponttól kezdve, amikor a keret szögsebessége megduplázódik.
A megoldás. Az e. stb. amely minden fordulóban megjelenik, megegyezik a mágneses fluxus első származékával a mínuszjellel vett idővel, azaz e = -Φt. N fordítás esetén e = -NΦt '. Mivel Φ = Φ0 ωs ωt, akkor:
Megtaláljuk az e. Pillanatnyi értékének függését. stb. az időtől:
Az e. stb.
Az e. stb.
Az e. stb. azt találtuk, hogy az e = Ԑ0 sin ωt egyenletben a t megfelelő értékét helyettesítjük. Számítsuk ki a pillanatnyi e. stb. t = 0,0050 s esetén:
Az e = NωΦ0 sinωt képletből látható, hogy ha az ω értéke kétszeresére növekszik, az e. stb. és a változás ciklikus gyakorisága az e. stb. növelje kétszer. Az e. stb. a következő képlet határozza meg:
ahol ω a kerék szögsebességének kezdeti értéke. Megtaláljuk az e1 = f (t) függést, mivel a szögsebesség két tényezővel nő:
Válasz. Az e. stb. amely a keretben keletkezik, az e = 62.8sin314t [V] képlet alapján határozható meg; az e. stb. Ԑ0 = 62,8 V; e. stb. ≈≈ 44,5 V; pillanatnyi értéke e. stb. mivel t = 0,0050 c egyenlő 62,8 V. Ha a keret forgási szögsebessége nő, az e pillanatnyi pillanatnyi értéke kétszerese. stb. az e1 = 125.6 sin 628t képlet alapján határozzuk meg.
Hány pólusú mágnesoszlop van egy 120 fordulat / perc teljesítményű hidrogenerátor forgórészével, ha a hidrogenerátor egy szokásos frekvenciájú váltakozó áramot generál?
Tekintettel: n = 120 ford./perc - a forgórész fordulatszámai percenként, v = 50 Hz - a váltóáram szokásos frekvenciája.
Keresse meg: p a mágneses pólusok száma.
A generátor forgórészének rotorfordulatszámát r / s-ban kifejezve végül:
Válasz. A hidrogenerátor rotorja 25 pár mágneses oszlopot tartalmaz.
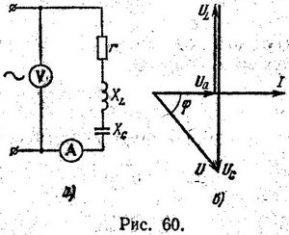
Amikor a tekercs a DC feszültség áramkör látható 12 árammérő áramerősség 4,0 A. Amikor ugyanazt a tekercs újra váltakozó áramú áramkör frekvenciája 50 Hz, és a feszültség 12 árammérő mutatja áram 2 , 4 A. Határozza meg a tekercs induktivitását. Melyik lesz egyenlő az aktív hálózati áram az, ha a sorozat a ka-hasított beleértve a kondenzátorok kerül 394 uF (ábra. 60 is)? Rajzolj egy vektordiagramot ebben az esetben.
Adott: UPOS = 12 V DC-feszültség, IPO = 4,0 A-teljesítményű DC FELSŐ = 12 V AC feszültségű, Iper = 2,4 A hálózati, v = 50 Hz-es váltakozó frekvenciájú , С = 394 * 10 -6 Ф-elektromos kapacitív kondenzátor.
Keresse meg: L - tekercs induktivitás; P az áram aktív teljesítménye.
Keresse meg a tekercs ellenállását:
A tekercs impedanciáját keressük:
Határozza meg az XL és L tekercseket, valamint az XC kondenzátor ellenállását:
Az áramkörben lévő kondenzátorral működő aktív áram a következő képlet alapján számítható ki:
ahol a kapcsolatot a kapcsolat határozza meg
A szükséges teljesítménytényezőt az alábbiak szerint kell meghatározni:
A numerikus értékek helyettesítésével kapunk:
P = 12 V * 2,4 A * 0,6 = 17,3 W
Mivel az Xc nagyobb, mint XL. akkor ebben az esetben a feszültségvektor φ szöggel elmarad az aktuális vektortól. Figyelembe véve, hogy az UC kétszer akkora, mint az UL, vektordiagramot (60.
Válasz. A tekercs induktivitása 12,7 mH, az áram aktív teljesítménye a 17,3 W tekercs és kondenzátor soros csatlakozásában van.