A vonalak és síkok kölcsönös elrendezésének axiómái az űrben
Az űrben lévő vonalak és síkok kölcsönös elrendezésének elmélete a következő axiómákon alapul.
Axióma 1. Ha három pont nem fekszik egy sorban, akkor keresztülmenő egy sík halad át.
Axióma 2. Ha egy síkban két egyenes pont fekszik, akkor ennek a vonalnak minden pontja a síkhoz tartozik. Ebben az esetben azt mondják, hogy a vonal a síkban fekszik.
Axióma 3. Ha két síknak van egy közös pontja, akkor közös vonaluk van ezen a ponton.
Az axióma 1 javításával járó sík tulajdonságait gyakran használják a gyakorlatban. A fényképezőgép állványának lábujjai ugyanarra a síkra tartoznak, ezért a kamera helyzete stabil. A két zsanérre rögzített ajtók nem foglalnak el egy bizonyos helyzetet, de ha hozzá egy harmadik rögzítési pontot - zárat, akkor az ajtók helyzete rögzítve van. Ha a szék lábfeje helytelenül van vágva, akkor a széklet három lábbal áll, a negyedik láb pedig a padló felett lóg.
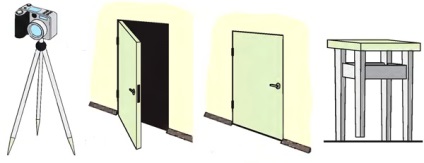
A gép tulajdonosa. amely axióma 2-t fejez ki, a rajzoló vonalzó egyenesének igazolására szolgál. A vonalzót az asztal felületére merőlegesen alkalmazzák: ha az él egyenesen van, akkor minden pont az asztal felszínével szomszédos, és ha egyenetlen, akkor van egy rés a vonalzó szélének és a táblázat felületének.
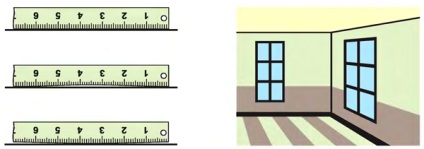
A 3-asxióma által rögzített sík tulajdonsága akkor jelenik meg, amikor metsződik a helyiség szomszédos falai.
Megjegyezzük, hogy a sztereometriában a planimetria összes axiómája és az összes kijelentés igazolt. Különösen az egyenlőség jelei és a háromszög hasonlóságának jelei továbbra is érvényesek a különböző síkokban fekvő háromszögekre. Az 1. axiómának megfelelően a síkot három A, B, C pont határozza meg, így néha a síkot három nagy latin betű jelöli: az A, B, C pontokon áthaladó síkot ABC jelöli.