Közvetlen és inverz geodéziai problémák a síkon
Ez - a gépen. Mert van egy közvetlen és visszafelé geodéziai feladat a földön ellipszoidon. Meg kell oldania őket a "Felsőfokú geodézia" során. Akkor meg fogja tudni a nagy különbséget. A Föld görbülete, alakja érezni fogja.
A név a „közvetlen” és „fordított” geodéziai problémák számos előre nem, de most a hagyományosan elfogadott és Felsőgeodézia egyszer és mindenkorra. Csak az egyik feladat az úgynevezett vonal a döntés, amely megállapította a pontok koordinátáinak terület, a másik - a hátsó, a döntést, amely ...
Ne menjünk előre.
Közvetlen geodéziai probléma.
Ismertesse az 1. pont (X1. Y1) koordinátáit, az 1-2 d12 vonal vízszintes helyzetét és az irányszögét # 945; 12 (7.3. Ábra). Meg kell találni a 2. pont koordinátáit. Ezek a közvetlen geodéziai probléma feltételei.
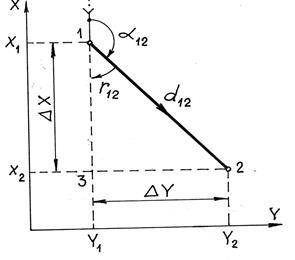
Ábra. 7.3. Közvetlen és inverz geodéziai problémák a síkon.
Egy közvetlen geodéziai feladatot használnak a tereppontok koordinátáinak meghatározására, különösen a teodolitikus tanfolyamok pontjai koordinátáinak meghatározásakor. Mivel ez a probléma egy síkban oldódik meg (a Gauss-Krueger vetületben), a 123 háromszög négyszögletes. Az 1-2 vonal orientált (a képen) a körkörös (# 945;) és negyed (r) rendszerekben. paraméterek # 916, X és # 916; Y nevezik a koordináták növekményeinek. A geometria és az elfogadott koordináta rendszer alapján írhatjuk ezt
Nyilvánvaló, hogy a lépték koordinátákat kell a jel „plusz” vagy „mínusz”, mert a koordinátákat a 2. pont lehet nagyobb vagy kisebb, mint a koordináta pont 1. Nem figyel a jelei a lépésekben koordinátákat, akkor írjon, derékszögű háromszög
Figyelembe véve a 3. ábrán látható rendszert. 6.3, ezt írjuk
azaz a koordináták növekményeinek jeleit a megfelelő irányszögek sin és cos funkcióinak jelei határozzák meg. Ezután az általános esetekben a képletek (7.1.) A formát veszik
7.1. Példa. Közvetlen geodéziai probléma.
Keresse meg a 2. pont koordinátáit.
Fordított geodéziai probléma.
Az inverz geodéziai probléma megfogalmazása. a két pont ismert koordinátáitól meg kell találnia a pontokat összekötő vonal vízszintes helyzetét és az irányszöget.
Az 1. ábrára hivatkozva. 7.3: az 1. és 2. pont ismert koordinátáitól keresse meg a d12 vízszintes távolságot és az irányszöget # 945;
Az inverz geodéziai problémát számos esetben alkalmazzák az eredeti irányok irányszögeinek meghatározásánál, valamint a terepen lévő mérnöki szerkezetek tervezési pontjai (geodéziai munka) megépítésével összefüggő különböző geometriai problémák megoldásában.
Meghatározzuk a koordináták növekményei és az irányszögek értékeinek kapcsolatát (7.2. Táblázat).
Az inverz geodéziai probléma megoldásához számítsa ki a koordináták növekményeit
ha az 1-2 irány irányszögének meghatározása feladata. Ha azonban meg kell határozni a 2-1 irány irányszögét, akkor a koordináták növekményeit képletek
Ezután számítsa ki a megadott irányú rumba értékét anélkül, hogy figyelembe veszi a koordináták növekményeinek jeleit
és a koordináták növekményeinek jelei alapján, a táblázat segítségével. 7.2, válassza ki a megfelelő képletet az irányszög kiszámításához.
A koordináták növekményeinek jelei az irányszög nagyságától függően
A azimut szög a vonal lehet meghatározni, ezáltal, az minden egyes célpontok, és azimut fordított irányban, ha szükséges, úgy határozzuk meg, a képlet az inverze a összehangolása a sarokban.
A 123 jobb oldali háromszög vízszintes távolságát a következő képletek találják:
Vízszintes számított távolság fenti képletekben, meg kell lényegében azonos egy kerekítési hiba.
7.2. Példa. Fordított geodéziai probléma.
Keresse meg az 1-2 irányú irányszöget és az 1-2. Vonal vízszintes helyzetét.
# 916; X2 = 9833.813 - 7273.856 = + 2559.957 m.
# 916; Y2 = 2165.041 - 5241.656 = -3076.615 m.
(Negyedik negyedév - NW) - lásd a táblázatot. 7.2.
Kisebb eltérések értékeit vízszintes távolság miatt kerekítési hibák, amikor kiszámítjuk az lépésekben a koordinátákat, és irány a szög.
Fordított irányszög.
Ezt a szöget is el lehet érni közvetlen számítással a megfelelő koordináta-növekményeken keresztül:
# 916; X1 = 7273.856 - 9833.813 = - 2559.957 m.
# 916; Y1 = 5241.656-2165.041 = + 3076.615 m.
(Második negyedév - SE) - lásd a táblázatot. 7.2.