Hogyan rajzoljunk
Táblázatok do alapvetően, hogy szemléltesse a kísérlet eredményei, és így legyen nagyon világos. Az alábbiakban adunk néhány általános tipp ábrázolásakor. A kísérleti adatokat kell ünnepelte félkövér, jól elkülöníthető pont. Példa megnézi 4. ábra mutatja.
Néha hasznos, hogy végezzen a kísérleti pontokat „legjobb” sima görbe.
Megjegyzés: a szó sima. A kezdők gyakran csatlakoztassa a kísérleti pontokat csak egy szaggatott vonal, mint az 5. ábrán látható. De így, mivel azt jelzi, hogy az arány a két érték közötti időszakos jellegű, és ez általában nagyon valószínűtlen. Inkább, az lenne várható, hogy ez az arány leírtak egy simább görbét (6. ábra),
A görbe szabályait kell követnie:
Minél több kanyarokban és egyenetlenségek a görbe, így kevésbé valószínű (csak írni kanyarvételkor nagy pontosságú mérést);
kiadások görbe olyannak kell lennie, hogy fekszik a lehető legközelebb a pontokat, és mindkét oldalán fordult megközelítőleg egyenlő számuk;
amennyire csak lehetséges ne legyen túl nagy eltérés a pontokat a görbe, akkor jobb, ha két vagy három kisebb eltérések, mint egy nagy.
Division védjegy a koordinátatengelyeken, ami a diagram adatai rámutat legjobb első ceruzát. Hirtelen úgy dönt, hogy változtatni a skála vagy kiderül, hogy egy bizonyos ponton véletlenül rosszul van beállítva.
Típusú mérés. Mérési hibákra típusai
Mérési mennyiséget nevezik a műveletet, aminek tudjuk, hogy hány alkalommal a mért érték több (vagy kevesebb) egy megfelelő értéket kell hivatkozni (mértékegység). Minden mérést lehet osztani két típusa van: a közvetlen és közvetett.
DIRECT - ezeket a méréseket, ahol mi érdekli közvetlenül mért fizikai mennyiség (tömeg, hossz, időintervallumokban hőmérséklet-változás, stb.)
Közvetve - ezeket a méréseket, ahol mi érdekli határozzuk (számított) direkt mérésekkel más változók az eredmények vele kapcsolatos bizonyos funkcionális függőséget. Például, sebességét meghatározó egyenletes mozgás a megtett távolság mérési időköz, mérése test sűrűsége és a testtömeg mérése térfogat, stb
A teljes mérési funkció - a képtelenség, hogy megkapjuk a valódi értékét a mért érték, a mérési eredmény mindig tartalmaz némi hiba (a hiba). Ezért, hogy jelezze, hogy az eredmény közel van az igazi érték, valamint a kapott eredmények azt mutatják, a mérési hiba.
Például, mértük a f fókusztávolságú lencse, és azt írta, hogy
Ez azt jelenti, hogy a fókusztávolság közötti tartományban 254-258 mm. De valójában ez az egyenlet (1) egy valószínűségi értelemben van csak bizonyos valószínűséggel, hogy így az (1) egyenlet kell egészíteni tovább részletezi a valószínűsége, amellyel ez a kapcsolat értelme (megfogalmazzuk ez az állítás pontosabb).
Általában számított abszolút és relatív hiba. Abszolút hiba Ax a különbség a valódi érték és a mért érték μ mérési eredmény X, azaz a
Az arány az abszolút hiba a valódi érték

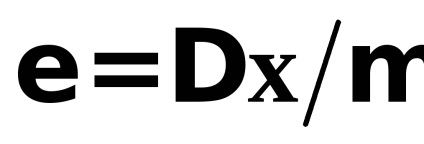
és az úgynevezett relatív hiba

Az abszolút hiba jellemzi a hiba a módszer és az intézkedések, amelyeket kiválasztottunk a mérésre.
A relatív hiba jellemzi a mérés minőségéről. mérés pontossága az úgynevezett kölcsönös a relatív hiba, azaz a 1 / ε.