Frances Hill OpenGL

Frances Hill "az OpenGL. Computer Graphics Programming. A szakemberek", 224. oldal

A konvex kombinációja vektorok konvex kombinációja fontos helyet foglalnak el a matematika és számos grafikus alkalmazásokhoz. A konvex kombinációja (konvex kombinációja) fordul elő további korlátozó kombinációt affinitás, nem csak az összeg a lineáris kombináció együtthatók egyenlőnek kell lennie egy, hanem minden együtthatót Továbbá meg kell nem-negatív. Így egy lineáris kombinációja (4.3) konvex, ha

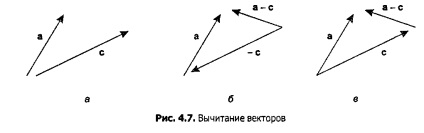
4.2. Áttekintés vektorok

Következésképpen, miközben<должны находиться между 0 и 1. (Почему?)

Így, 0,3A + 0,7b konvex kombinációja a vektorok a és b, míg a 1,8a - 0,8b - nincs. Ava2 együtthatókészlet. Ez néha egy partíció az egység (partíció egység), ami azt jelenti, hogy ez az egység mennyisége „anyag” darabokra tört. Konvex kombinációja gyakran merülnek fel olyan alkalmazásokban, ahol valaki egy egységnyi mennyiségű „mix”, és össze lehet csak pozitív szám a különböző összetevőket. Az ilyen kombinációk jelennek meg a legváratlanabb helyzetekben. Például, látni fogjuk, a 11. fejezetben, hogy a spline görbék valóban konvex kombinációja egyes vektorok és az általunk vizsgált szín (12. fejezet) megtudjuk, hogy minden egyes fényerőt is képviselteti magát egy konvex kombinációja három egyszerű színek!

Úgy tűnik, hasznos fogalma „a készlet minden konvex kombináció” egy sor vektorok. A két vektor V4 és v2 a készlet minden konvex kombinációk a készlet minden vektorok formájában

ahol a paraméter változhat és a 0-ról 1 (miért?) Milyen a sok? Átalakítása az egyenlet (4.6), kapjuk:

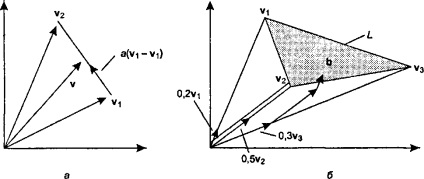
Ábra. 4.8. A készlet vektorok is képviseli konvex kombinációi ábra. 4.8 ábra egy v vektor, egyenlő az összege v, és néhány része \ 2- v. és a végén a v vektor található, az összekötő vonal v, és v2. Mivel a változás 0-1, a végén v lehet elfoglalni pozíciókat, amelyek egybeesnek az összes pontot a összekötő szakasz a végén v, v2, és csak azokat a rendelkezéseket.