tavaszi inga
Rezgési folyamat, amely meg kell felelniük, vannak osztva periodikus és nem periodikus, jellegétől függően az időbeli változását a fizikai mennyiségek jellemző a rendszer állapotát. És ezért az előfordulási ingadozások vannak osztva a szabad és erőltetett.
Free (magán) oszcillációk nevezik rezgések merülnek fel a rendszer eredményeként egy kezdeti eliminációs stabil egyensúlyi állapot. Ha szabad rezgések a rendszerben mindig hatnak (általában ok), hajlamos visszatérni a rendszer egyensúlyi helyzetébe. (Abban az esetben, ingadozások a terhelést a rugós visszaállító erő egy rugalmas rugó erő.)
Ha a rendszerben nincs súrlódási erő, és minden egyéb akadály a szabad rezgések, nincs veszteség a mechanikai energia és rezgés is előfordul a végtelenségig egy állandó amplitúdóval. Ezek a rezgések az úgynevezett szabad csillapítatlan. Csillapítatlan rezgések rezgések idealizált esetben. Szabad rezgések valós rendszerek mindig csillapítani. A csillapító rezgések elsősorban az intézkedés a súrlódási erők a rendszerben. Tartós oszcillációk a valós rendszer által gerjesztett befolyása rá változó külső erő. Ebben az esetben a rezgések nevezzük belsőleg.
Úgynevezett periodikus rezgések, amikor az értékek az összes fizikai mennyiségekkel módosulhatnak oszcilláció ismétlődnek rendszeres időközönként. A legkisebb ilyen időkülönbség, amely után az összes érték ismételt mennyiségekben jellemző oszciiiáiómozgásban nevezzük időszak rezgések. Ezalatt az idő alatt, azt mondják, hogy végre egy oszcilláció.
Időszakos rezgési frekvencia a rezgések száma egységnyi idő alatt. Ha során a rendszer rezgésbe, akkor a rezgési frekvenciája megegyezik :. Tekintettel arra, hogy egy ideig azonos időszakban egy oszcilláló végzünk, akkor érkezik a kommunikáció gyakorisága időszakra:
A frekvencia mértékegysége a Hertz (Hz). Az 1 Hz frekvencia elfogadja ezt oszcilláció folyamatot, amelyben egy második végeztünk egy teljes oszcillációs (Hz = 1 / s).
Egy konkrét esetben a periodikus rezgések harmonikus vibráció, amelyben egy oszcilláló fizikai mennyiség (például, a koordináta a rugóterhelés) változik időben szerint a cosinus (vagy szinusz):
ahol a mennyiség megegyezik a legnagyobb abszolút értéke a fluktuáló nevű értéket amplitúdója az oszcillációk. Expression meghatározza az értéket adott időben, és az úgynevezett fázis ingadozások. A kezdeti fázisban van a kezdeti szakaszban.
Érték az úgynevezett ciklikus frekvencia harmonikus rezgés.
Időszakban a funkció (1), mint ismeretes a matematika
- ez lesz az időszak oszcilláció. A frekvencia a harmonikus rezgés van:
Megjegyezzük, hogy a függvény (1) egy olyan megoldás a differenciálegyenlet:
ahol - a második deriváltja az idő függvényében.
;
és behelyettesítve a (2) egyenlet válik valódi egyenlőség, szükség szerint.
A matematika, ha bebizonyosodik, hogy (1) az egyetlen megoldás, hogy a differenciálegyenlet (2). Így, ha a rezgés az oszcilláló mozgást létrehozó fizikai mennyiség bármikor, a (2) összefüggés. A rezgések harmonikus és előfordulhat időszakra
Értékei az állandók és határozzuk meg, mint egy szabály, a kezdeti feltételek.
A Lab 2 Be kell, hogy vizsgálja meg kísérletileg a szabad rezgések egy rugó és egy matematikai inga.
Tavaszi inga. kísérleti eljárás
Tavaszi inga nevezzük a test felfüggesztve egy rugó. Legyen egy rugóállandó felfüggesztett teher súlya (1. ábra)
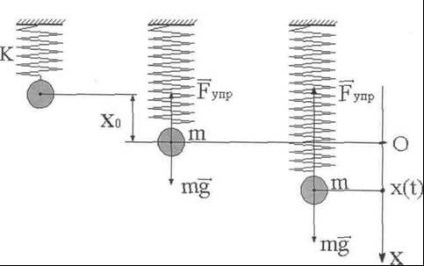
Tekintsük a függőleges mozgását a rakomány, amely akkor történik, miután egy kis lökést hatására egy rugalmas rugó és a gravitáció. Tavaszi vállalja a fény és a tömege elhanyagolható. Szintén figyelmen kívül hagyjuk az erő a légellenállás, tekintve alacsony.
Rezgő fizikai mennyiség ebben a példában az a koordináta a terhelést. Az eredetük a referencia tengelyen egy pont terhelésnek megfelelő egyensúlyi helyzet (1. ábra). Ebben a helyzetben, a rugó már feszített meghatározott összeggel az egyensúlyi állapot
Amikor mozgó áruk a egyensúlyi helyzetben, például le, hogy a távolság eltekintve ez a gravitáció miatt
az erő rugalmassági egyenlő szerinti Hooke-törvény, amint az 1. ábrán látható nem.
Az egyenlet Newton második törvénye a terhelést a vetülete a tengelyen:
Figyelembe véve kapcsolatban (3), az egyenlet Newton második törvénye a forma
amelynél a nyúlvány a gyorsulás semmi tengelye, a második idő szerinti deriváltja a koordinátáit a rakomány, azaz a . Így azt találjuk, hogy egy adott ideje alatt a terhelés ingadozása annak koordinátáit a kapcsolat
Ezért ezeket a rezgéseket a harmonikus és melyek fordulnak elő gyűrűs gyakorisága
A kísérlet során, meg kell győződnie arról, hogy a határidő terheléstől független ingadozások a mért amplitúdó, időtartam oszcilláció és az ismert érték terhelés számított tömeg rugóállandó összhangban kapcsolatban (5) a következő képlet
Annak megállapításához, a tavaszi ráta és lehet egy másik módszer. Ebből a célból meg kell mérni a feszültséget a tavaszi egyensúlyi helyzetében a terhelést, és a (3) egyenlet, ahol
Miután becslési hibák, a kapott értékeket össze kell hasonlítani egymással, és elmagyarázni, ha szükséges, egy esetleges eltérés okozza.