A rugós inga szabad oszcillációi
A munka célja. Megismerni a csillapított és csillapított, szabad mechanikus rezgések fő jellemzőit.
A feladat. Határozza meg a rugós inga természetes ingadozásainak időtartamát; ellenőrizze az időszak négyzetének linearitását a tömeghez viszonyítva; meghatározza a rugó merevségét; határozza meg a csillapított oszcillációk időtartamát és a rugó inga csillapításának logaritmikus csökkenését.
Eszközök és tartozékok. Egy állvány, egy méretarányú, egy rugó, egy sor rakomány különböző tömegek, egy hajó vízzel, a stopper.
1. A rugós inga szabad oszcillációi. Általános információk
Az oszcillációk olyan folyamatok, amelyekben egy vagy több fizikai mennyiségek periodikusan megváltoztatják ezeket a folyamatokat. Az oszcillációkat különböző időperiódusú idő függvényekkel lehet leírni. A legegyszerűbb oszcillációk a harmonikus oszcillációk - olyan oszcillációk, amelyekben az oszcilláló mennyiség (pl. A rugó terhelésének elmozdulása) idővel a koszinusz vagy a sinus törvénye szerint változik. A külsõ rövid távú erõ rendszerének akciója után keletkezõ oszcillációk szabadnak tekintendõk.
Vegyük figyelembe az egyik legegyszerűbb oszcilláló rendszert - egy rugós inga, amely tömege m. rugalmas rugóval felfüggesztve k merevségi együtthatóval
(1. ábra). Legyen 0 a rugó hossza, függőleges terhelés nélkül. Amikor szuszpendáló a rakomány a gravitáció rugó van nyújtva, hogy x 1 úgy, hogy az inga egyensúlyban lesz, mert a egyenlőség mg gravitációs modulok és a rugalmas erő F Ex: mg = kx 1, hajlamos visszatérni a terhelést az egyensúlyi helyzet (feltételezve, hogy az alakváltozás a rugó tökéletesen rugalmas és engedelmeskedni Hooke törvényének).
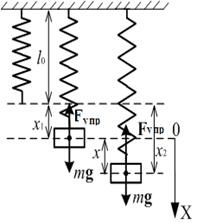
Ha a terhelést az egyensúlyi helyzetből visszavonjuk, az x eltérítésével. akkor a rugalmasság ereje növekszik: F упрпр = - kx 2 = -k (x 1 + x). Az egyensúlyi helyzet elérése után a terhelés nem nulla sebességgel és az egyensúlyi helyzet a tehetetlenséggel halad át. Amint a mozgás folytatódik, az egyensúlyi helyzetből való eltérés növekedni fog, ami a rugalmas erő növeléséhez vezet, és a folyamatot az ellenkező irányba megismétlik. Így a rendszer oszcilláló mozgása két okból következik be: 1) a test vágya, hogy visszatérjen az egyensúlyi helyzetbe, és 2) a tehetetlenség, amely nem teszi lehetővé a test számára, hogy azonnal álljon meg az egyensúlyi helyzetben. Súrlódási erők hiányában az oszcilláció korlátlan ideig folytatódna. A súrlódási erő jelenléte arra vezet, hogy a vibrációs energia egy része belép a belső energiaba, és az oszcilláció fokozatosan bomlik. Az ilyen oszcillációkat elnyomják.
Nyugtalan szabad oszcilláció
Először is vegyük fontolóra egy olyan rugós inga rezgését, amelyen a súrlódási erők nem működnek - csillapodva szabad oszcillációkat. Newton második törvénye szerint, figyelembe véve az X tengelyen lévő vetületek jelét
Az egyensúlyi állapotból a gravitáció által okozott elmozdulás :. Az (1) egyenletben történő helyettesítéssel:. Ennek az egyenletnek a jobb és a bal oldalait m-vel osztva, feltételezve, hogy a = d2x / dt2. megkapjuk a differenciálegyenletet
Ezt az egyenletet egy rugós inga harmonikus oszcillációjának differenciálegyenletének nevezik. Ebből az egyenletből következik, hogy megszűnése után a külső fellépés, ami a kezdeti elutasítása a rendszer az egyensúlyi helyzetből, a mozgás az áruk miatt kizárólag a rugalmas erő (gravitációs erő hatására a DC offset).
A homogén másodikrendű differenciálegyenlet (2) általános megoldása formában van
Ezt az egyenletet harmonikus oszcillációs egyenletnek nevezzük. A terhelés legnagyobb eltérését az egyensúlyi helyzetből A 0 az oszcillációk amplitúdójának nevezzük. A koszinusz argumentumának mennyiségét az oszcilláció fázisa nevezik. konstans # 966; 0 a kezdeti időpontban (t = 0) lévő fázisértéket jelenti, és az oszcilláció kezdeti fázisa. érték
a természetes oszcillációk körkörös vagy ciklikus frekvenciája van. a T oszcilláció periódusával kapcsolódik a relációhoz. Az oszcillációs periódus meghatározása
Tekintsük a rugós inga szabad ingadozását súrlódási erő (csillapított oszcilláció) jelenlétében. A legegyszerűbb és egyidejűleg a leggyakrabban előforduló eset, a súrlódási erő arányos a sebességgel # 965; mozgás:
ahol r állandó, az ellenállási együttható. A mínusz jel azt mutatja, hogy a súrlódási erő és sebesség ellentétes irányú. A Newton második törvényének egyenlete a vetületben az X tengelyre rugalmas erő és súrlódási erő jelenlétével
Ez a differenciálegyenlet a # 965; = dx / dt írható
hol van a csillapítási együttható? Az adott oszcillálórendszer szabad csillapított rezgéseinek ciklikus frekvenciája, azaz energiaveszteség hiányában (# 946; = 0). A (8) egyenletet a csillapított oszcillációk differenciálegyenletének nevezzük.
Az x elmozdulás függésének megszerzése a t időpontban. meg kell oldani a differenciálegyenletet (8). Kisebb csillapítás () esetén az egyenlet megoldása az alábbiak szerint írható le:
ahol A 0 és # 966; 0 - az induló amplitúdó és az oszcilláció kezdeti fázisa;
- a csillapított rezgések ciklikus frekvenciája # 969; >> # 969; ≈ # 969; 0.
Ebben az esetben a rakomány mozgása frekvenciájú harmonikus oszcillációnak tekinthető # 969; és változó amplitúdó, a törvény szerint változó:
A függvény (9) grafikonján, A szaggatott vonalak a csillapított oszcillációk amplitúdójának (10) változását mutatják.
Ábra. 2. A terhelés x eltolódásának függvénye a t időpontban súrlódó erő jelenlétében
Az oszcillációk csillapítási mértékének számszerűsítése céljából egy olyan mennyiséget kell megadni, amely egyenlő az egy adott periódustól eltérő amplitúdók arányával, és csillapítás-csökkentésnek nevezzük:
Ennek a mennyiségnek a természetes logaritmusa gyakran használatos. Ezt a paramétert nevezik a csillapítás logaritmikus csökkenésének:
Ha az amplitúdó t-rel egy t tényezővel csökken, akkor a (10) egyenletből következik
Ezért a logaritmikus csökkenéshez a kifejezést kapjuk
Ha az amplitúdó e t tényezővel csökken a t 'idő alatt (e = 2,71 a természetes logaritmus alapja), akkor a rendszernek ideje van arra, hogy az oszcillációk számát
Következésképpen a logaritmikus csillapítás csökkenés az oszcillációk számának kölcsönös volta, amely során az amplitúdó egy e tényezővel csökken. Annál többet # 952;, annál gyorsabban csökken az oszcilláció.
2. Kísérleti eljárás és kísérleti beállítás
Ábra. 3. Telepítési rajz
A telepítés egy 1 állványból áll, 2 mérési skála segítségével. A 3 rugó állványára négy különböző tömegű terhelést töltünk be. A 2. feladatban a csillapított rezgések vizsgálatakor egy 5 gyűrűt használnak a csillapítás fokozására, amelyet egy átlátszó 6 edényben vízzel helyeznek el.
Az 1. feladatban (vízzel és gyűrűvel ellátott edény nélkül) az első megközelítésben az oszcilláció csillapítását elhanyagolhatjuk és harmonikusnak tekinthetjük. Az (5) képlet alapján a harmonikus oszcillációra vonatkozóan a T2 = f (m) függvény lineáris, amiből a k rugós merevségi koefficiensét a
hol van a T 2 egyenes meredeksége m-ből.
1. feladat: A rugós inga természetes ingadozásainak a terhelés tömegére gyakorolt függésének meghatározása.
1. Határozza meg a rugós inga oszcillációs idejét a terhelés tömegének különböző értékeire. M. Ehhez használd a stopperórát minden egyes m értékhez, hogy megmérjük az összes n oszcilláció t időpontját (n ≥ 10) háromszor, és kiszámítsuk az időtartamot az átlagos időből. Az eredményeket a táblázat tartalmazza. 1.
2. A mérési eredményekből a T2 periódus négyzetét ábrázolja a tömeg m. A grafikon szögszeletéből határozzuk meg a rugó rugalmasságát (16).
A természetes oszcillációk időtartamának meghatározására szolgáló mérések eredményei
3. Kiegészítő feladat. Becsülje meg a véletlenszerű, teljes és relatív értékeket # 949; t időmérési hiba a tömegértékhez m = 400 g.
2. feladat: A rugós inga logaritmikus csökkenésének csökkentése.
1. Felfüggeszteni a rugót tömege m = 400 g gyűrűvel, és tegye egy edénybe vízzel, hogy a gyűrű teljesen a vízben legyen. Határozza meg az elnyomott oszcillációk időtartamát egy adott m értéke tekintetében az 1. feladat 1. pontjában leírt módszer szerint. A méréseket háromszor meg kell ismételni, és a táblázatban a bal oldali részen rögzített eredményeket. 2.
2. Húzza ki az inga az egyensúlyi helyzetből, és jelezze az első amplitúdóját a vonalzó mentén, mérje meg a t 'időt. amelynek során az oszcillációk amplitúdója 2-szeresére csökken. Mérje meg háromszor. Az eredményeket a táblázat jobb oldalán találjuk meg. 2.
3. A (14) képlet segítségével számítsuk ki a csillapítás logaritmikus csökkenését # 952, figyelembe véve, hogy ln2 = 0.693.
hogy meghatározzuk a csillapítás logaritmikus csökkenését
Az oszcilláció periódusának mérése
amplitúdó csökken 2-szer
4. Vizsgálja meg a kérdéseket és feladatokat
1. Milyen oszcillációkat mondunk harmonikusnak? Adja meg főbb jellemzőik meghatározását.
2. Milyen hullámzásokat hívnak elhalványulnak? Adja meg főbb jellemzőik meghatározását.
3. Mutassa be a logaritmikus csökkenéscsökkentés és a csillapítási együttható fizikai jelentését.
4. Derítse ki a terhelés gyorsaságának és gyorsulásának függését egy rugón, amely harmonikus rezgéseket hajt végre. Hozd a diagramokat és elemezd.
5. Végezze el a függőségeket a terhelés kinetikus, potenciális és teljes energiájának idején, a rugón oszcillálva. Hozd a diagramokat és elemezd.
6. A szabad oszcilláció differenciál egyenletét és annak megoldását.
7. Harmadik oszcillációk grafikonjait a π / 2 és π / 3 kezdeti fázisokkal kell megrajzolni.
8. Milyen mértékben változhat a logaritmikus csillapítás csökkenése?
9. Adja meg a rugócsillapítás és a megoldás csillapított oszcillációinak differenciálegyenletét.
10. Milyen joggal változtatja meg a csillapított rezgések amplitúdóját? Csillapított oszcillációkat időszakosan?
11. Milyen mozgást neveznek aperiodikusnak? Milyen feltételek mellett figyelhető meg?
12. Mi a természetes oszcillációs frekvencia? Hogyan függ az oszcilláló test tömegétől a rugós inga számára?
13. Miért alacsonyabb a csillapított rezgések frekvenciája, mint a rendszer természetes oszcillációinak gyakorisága?
14. A rugó felfüggesztése esetén a rézgömb függőleges rezgéseket okoz. Hogyan változik az oszcilláció periódusa, ha az alumínium felfüggesztése ugyanabban a sugárban helyezkedik el, mint egy rézgolyó?
15. A mi érték logaritmikus dekrementálás rezgéseket csillapítani gyorsabb: a # 952 1 = 0,25, vagy # 952; 2 = 0,5? Hogy ezeket a grafikonokat csillapodó rezgések.
3. Ahmatov A. Laboratory gyakorlati a fizika /.
- M. Executive. wk. 1980. - 359 p.