3. feladat
Számítsa ki és vizsgálja meg az elágazó egyenáramú elektromos áramkört az első és a második Kirchhoff-törvény és a kontúráram-módszer segítségével.
Az elágazó áramkör kiszámításához fontos a láncban lévő ágak és csomópontok száma.
Az elektromos áramkör egy ágát olyan szakasz képezi, amely csak a sorosan kapcsolt elemekből áll.
Egy állandó áram folyik az ágon, az ág két csomópontot köti össze.
Az elektromos áramkör csomópontja több ágág összekapcsolási pontja, amelyben az áram elágazik.
Az EWB programban, # 8810; csomópont # 8811; más jelentése van, az áramkörnek bármely pontja nulla lehet, és más csomópontok potenciálja. Így az áramkörök elméletével összhangban lévő egyik ágnak nincs csomópontja, míg az EWB programban a 3. ábrán több csomópont lehet egy ágon.
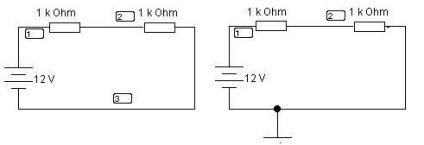
Ábra. 3. Egy koncepció példája # 8810; csomópont # 8811; az EWB programban.
A bal oldalon látható (3. Ábra), hogy a földeletlen áramkörben a program három potenciális csomópontot határoz meg, a csomópont által földelt szakasz nem tekinthető, - (1. Az áramkörök elmélete szempontjából a fenti áramkör csomópontja csak a jobb oldalon található, a föld csatlakozási pontján (1.
Amikor a csomópontokban összekötött ágakat keresztezük, zárt kontúrt nyerhetünk.
A zárt kontúr egy több ágon áthaladó zárt útvonal, és a vizsgált kontúr minden csomópontja egyszerre jelentkezik.
Kirchhoff első törvénye a csomópontokra vonatkozik, és a következőképpen fogalmazódik meg:
A csomóponton az áramok algebrai összege nulla
Egy algebrai összeget hívunk, mert a csomóponthoz viszonyított aktuális irányt figyelembe kell venni. Minden csomópontra irányított áramlat egy jelet tartalmaz, és a csomóponttól irányított - az ellenkezővel. Kirchhoff első törvényét másképp lehet megfogalmazni:
A csomópontba áramló áramok összege megegyezik a kimenő áramok összegével
Kirchhoff első törvényének fizikai jelentése, hogy a töltés felhalmozódása nem fordulhat elő az elektromos áramkör csomópontjaiban.
Kirchhoff második törvénye az elektromos áramkör zárt áramkörére vonatkozik, és a következőképpen fogalmazódik meg:
Minden zárt kontúrban a feszültségek algebrai összege
az áramkör elemei megegyeznek az emf összegében ebben az áramkörben
Ebben a definícióban azt is hangsúlyozzák, hogy az összegnek algebrailag kell lennie, ez azt jelenti, hogy figyelembe kell venni a feszültségek és az EMF jeleit, amelyek a feszültségösszegbe kerülnek. Zárt hurokban az áram csak egy irányban mozoghat, ezért az áramlás irányát kell kiválasztani. Ezt követően a kontúr a kiválasztott irányba halad, és a feszültségcsökkenés az elemen vagy az EMF forrásán pozitívnak tekinthető, ha az áramlat az elemen vagy az EMF-en keresztül megegyezik a bypass irányban. Ellenkező esetben a megfelelő feszültségeket és az EMF-et az ellenkező jelkel összegezzük.
Kirchhoff törvényei alapján összeállítják az ismeretlen ágak áramlási egyenleteit. A kapott egyenletek rendszere lineáris, megoldása lehetővé teszi számunkra, hogy ismeretlen áramokat keressünk a lánc ágaiban. A számítás eredményét ellenőrizni lehet az EWB programban, az ampermérők csatlakoztatásával a megfelelő ágak megszakításához.
A számítással kapcsolatos vázlatos diagramokat a 4. táblázatban, a feladatok változataiban és az ellenállások névleges értékeiben és az EMF forrásokban az 5. táblázatban adjuk meg.
A munka előrehaladása
1. A bevezetésben megfogalmazzuk az alkalmazott elméleti alapelveket;
2. Határozza meg a kiszámítás kezdeti adatait: a kapcsolások sémáját, az ellenállások és az EMF források értékeit;
3. Adja meg a csomópontok, kontúrok szimbólumát. Állítsa be az áramlások irányát és a kontúrok kijátszását az óramutató járásával megegyező irányba, rajzolj diagramot a jelzéssel;
4. Egy egyenletrendszer összeállítása Kirchhoff első és második törvénye szerint;
5. Készítsünk egy egyenletrendszert hurkáramokra és egyenleteket az ágak áramának meghatározására;
5. Hozza az egyenletek rendszerét a standard formához, beleértve mindegyiket
az egyenlet ismeretlen;
6. Válassza ki a megoldás módját az egyenletek rendszerének megoldásához, a megoldás végrehajtásához, a választott módszer által vezérelve, a megoldás előrehaladásával a jelentésben szereplő kulcsfontosságú átalakításokkal és magyarázatokkal;
7. Ha bizonyos áramokra negatív áramokat kapunk, rajzoljunk egy új áramkört korrigált áram irányokkal;
8. Végezze el a megoldás ellenőrzését az eredeti egyenletekben található ismeretlenek helyettesítésével, ha nem teljesíti az ellenőrzési feltételeket, ismételje meg a számítást és keresse meg a hibát;
9. Szerelje össze az áramkört az EWB-ben. Mérje meg a keresett áramokat az ampermérők beépítésével a vizsgált áramkör minden ágában és a feszültségcsökkenésnek az összes áramköri ellenállással szemben;
10. A számítások és a mérések eredményeit a 6. táblázatban foglalják össze;
A kutatási számítások eredményei
Aktuális számítási módszer
Az áramlatok és feszültségek kiszámításának eredményei a lánc ágaiban.
Az áramlások és feszültségek mérése a láncágakban.