Differenciálegyenletek megoldásának módszerei, a véges különbségek módszerei
Az előnye, hogy ezeket a módszereket, hogy csökkentik a megoldás a határ érték probléma egy differenciálegyenlet egy algebrai egyenletek az ismeretlen függvény értékeit egy adott ponthalmaz. Ez úgy érhető el, hogy a differenciálegyenletet bejövő származékokat a véges differenciál approximációjukkal helyettesítik.
Tekintsük egy ilyen megoldási módszer lényegét egy másodikrendű differenciálegyenlet (1,41) vonatkozásában adott határfeltételek esetén (1,42). A szegmenst [0,1] n egyenlő részre osztjuk az xi = ih (i = 0,1, n) pontokkal. A határértékprobléma (1.41), (1.42) megoldását a xi csomóponthoz tartozó yi rácsfüggvény értékének kiszámítására redukáljuk. Ehhez a belső csomópontok egyenletét (1.42) írjuk:
Ezeket a kapcsolatokat a véges különbségű közelítésekkel helyettesítjük:
Ha ezeket a kifejezéseket (1.49) helyettesítjük, akkor különbség-egyenletrendszert kapunk:
(i = 1) és yn (i = n - 1) esetén a határkörülményekből (1.42):
A gyakorlatban a határkörülmények gyakran általánosabb formában (1.38) vannak meghatározva:
Ebben az esetben a határfeltételeket a differenciál formában is ábrázolni kell az Y '(0) és az Y' (1) származékok finomkülönbség-viszonyokkal történő közelítésével. Ha egyoldalú különbségeket használnak (a megfelelő mintát az 1.7a. Ábra mutatja), amelyek esetében a származékokat a pontosság első sorrendjével közelítik meg, akkor a különbségi határfeltételek formája
Ezekből a kapcsolatokból az y 0, yn értékeket könnyen megtalálhatjuk.
Rendszerint azonban célszerű közelíteni a (1.52) pontban szereplő származékokat a második pontossági sorrendhez a központi különbségek segítségével:
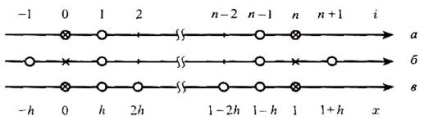
Ábra. 1.7. A határfeltételek közelítése
Az expressziós adatok értékeket tartalmaz a háló funkciót és yn + 1 az úgynevezett fiktív csomópontok X = 1-h = 1 és x + H, kívül fekszik a szegmens vizsgált (ábra. 1.7, b). Ezekben a csomópontokban meg kell találni a kívánt funkció értékeit is. Ennek következtében a gridfunkció ismeretlen értékeinek száma kétszeresére nő. A rendszer bezárásához két további különbségegyenletet (1.51) vonzanak i = 0, i = n esetén.
Meg lehet közelíteni a határfeltételeket a második sorrendhez más módon (lásd az 1.7., C. Ábrát). Ebben az esetben közelítéseket használnak:
Így a differenciálegyenlet határértékei megoldásának megoldása az (1.51) képlet algebrai egyenletrendszerének megoldására korlátozódik. Ez a rendszer lineáris vagy nemlineáris, attól függően, hogy a differenciál egyenlet lineárisan vagy nemlineárisan (1,41). Az ilyen rendszerek megoldásának módszereit korábban tekintették.
az űrlap határfeltételeivel
A 0,1-es intervallumot a h csomópontokkal állandó h lépcsővel osztjuk fel. A második Y2 származékot közelítjük a véges különbséghez viszonyítva (1,50). Ebben az esetben az Y (xi) csomópontokon lévő ismeretlen függvény értékeit körülbelül az yi rácsfüggvény megfelelő értékei váltják fel. Írd az egyenletet (1.54) minden egyes csomóponthoz a jelzett approximációk segítségével
Legyen pi és fi a mennyiségek, ill. Az egyszerű átalakítások után az utolsó egyenletet csökkentjük az űrlapra
Elértük az n-1 lineáris egyenletrendszert, amelynek száma megegyezik a csomópontok gridfunkciójának ismeretlen értékeivel. Az intervallum végén lévő értékeket a határfeltételek határozzák meg (1,55):
Az egyenletek rendszerének (1.56) megoldásával, a feltételek (1.57) figyelembe vételével, megtaláljuk a rácsfüggvény értékeit, amelyek megközelítőleg megegyeznek a kívánt funkció értékével. Megmutatjuk, hogy egy ilyen megoldás létezik, és egy pontos megoldáshoz konvergál, mint h → 0.
A megoldás létezésének bizonyításához a lineáris egyenletek rendszerét (1.56) tekintjük. Mátrixa tridiagonal; A fő átlós elemek. Mivel a p (x)> 0, pi> 0 és a mátrix diagonális elemei dominálnak a többiek fölött, mivel mindegyik sorban ezeknek az elemeknek a modulja nagyobb, mint a két másik elem moduljának összege, amelyek mindegyike egyenlő egyvelettel. Amikor ez a feltétel teljesül, a lineáris egyenletek rendszerének megoldása létezik és egyedülálló.
Ami a megoldás konvergenciáját illeti, az alábbi állítások érvényesek.
Jóváhagyása. Ha a p (x) és f (x) függvények kétszer folyamatosan differenciálhatóak, akkor h + 0-ra a differenciálódás egyenletesen konvergál a pontos értékhez O (h2) sebességgel.
Ez elegendő feltétel a határérték-probléma (1.54), (1.55) véges differenciálódási módjának konvergenciájához.
Egy lineáris algebrai egyenlet (1.56) egy tridiagonális mátrix segítségével egy sweep módszerrel megoldható. Ebben az esetben a p (x)> 0 feltétel biztosítja a futtatás stabilitási feltételeinek teljesítését.
Ezt a módszert alkalmazzák a p (x)<0, хотя успешный результат заранее предвидеть трудно. Для оценки получаемого решения в этом случае необходимо провести расчеты для разных значений шага (не менее трех) и убедиться в том, что полученные значения функции в одних и тех же узлах близки между собой и разность их уменьшается, что говорит о стремлении решения к некоторому пределу при h → 0.
A lineáris egyenlet legegyszerűbb esetét tekintettük. Sokkal nehezebb megoldani a nemlineáris problémákat. A határérték-problémát egy másodrendű egyenletnek tekintjük:
A véges különbség módszerével különbségi nemlineáris egyenletrendszereket kapunk
A különbségi rendszerek elméletében bebizonyosodott, hogy a differenciaegyenletek (1.59) által meghatározott különbség-megoldás a pontos megoldáshoz közelít, mint h → 0. A konvergencia elégséges feltétele a forma
A nemlineáris algebrai egyenletek rendszere (1.59) iteratív módszerekkel oldható meg. Ennek megoldására a linearizációs eljárást is alkalmazzuk, azaz Nemlineáris rendszer oldatának redukálása lineáris algebrai egyenletek rendszerének sorrendjéhez.
Legyen a rendszer megoldása (1.59) a k-iterációban. Ezután a rendszer jobb oldalán (1.59) lévő ismert értékek helyettesítjük
Következésképpen lineáris algebrai egyenletek rendszerének megoldására jutottunk az yi értékekhez viszonyítva (k + 1) - iterációban. Mivel a rendszer mátrixa tridiagonalis, mindegyik iterációnál sweep módszerrel lehet megoldani. Csak néhány kezdeti közelítést kell megadni; az y0, yn értékeket a határfeltételek határozzák meg (1,60).
Megjegyzendő, hogy ez az iteratív folyamat konvergenciája meglehetősen lassú. A konvergencia elégséges feltétele a forma
Ez a feltétel, valamint a feltétel (1.61) korlátozza az eredeti egyenlet (1.58) f (x, Y) jobb oldalát.