9. osztályba
Kör a készlet minden pont a síkon egyenlő távolságra egy ponton, a központ (1.).
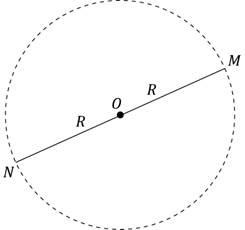
Ábra. 1. Egy R sugarú kör középpontja egy ponton O
Mi a kerülete?
Mivel nem elasztikus szál a kör alakú, vágd kiegyenesedik a végeit, hogy vágja, a hossza ebben a szegmensben, és ad egy ötlet kerületének hosszával.
Az említett menet található a kör pontatlan, véges méretei, nem tudjuk használni ezt a szálat mérni a nagyon kis körben, például az elektron pályáját, vagy nagyon nagy kört, például a Föld pályáját, stb
Ie használt képlet legitimálja annak szükségességét, hogy először is meg kell érteniük, hogy tisztázza, mi a kerülete? Meg lehet mérni, és ez nem az ókori görög tudós Archimedes vissza a III században tanulmányozása az arány a kerülete, hogy az átmérő ().
Azt empirikusan találta, hogy ez az arány állandó vagy közel állandó a kerülete mérések, és nagyjából egyforma. Megállapítást nyert, hogy a kerülete átmérője állandó valamennyi kerületét. Ez a szám jelöli a görög betű ()
Ezt bizonyítja, hogy - egy irracionális szám, azaz leírható egy végtelen tizedes aperiodikus, a közelítő érték 3,1416 .... Miben különbözik attól az értéktől, amely megtalálható Archimedes (az 3,1416)? Pontosság körülbelül egyenlő 0,002.
Let - kerülete? Így ez a képlet már használják, figyelembe véve, hogy. A kérdés jogos, mondhatjuk a hossza a kerülete, de nem tudom, mi ez, mert a megadott menet, amely használt Archimedes ad egy vizuális ábrázolás a kör. Kiderült, hogy képesek vagyunk úgy a hossza a kerülete, de mi az, nem tudjuk.
Tisztázni kell, hogy ez a kerülete. Emlékezzünk: hossza közelítőleg egyenlő bármilyen sokszög görbe, ami lépett, vagy a közelébe ismertet.
Kerülete körül egy kört, és lehet feliratos gon, mi gon beírását a jogot arra, hogy egy kör (2. ábra) - hossza oldalán - az oldalak számát.
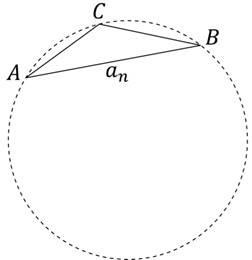
Ábra. 2. N-gon írt kör
A kerülete a háromszög-szer nagyobb, mint a perem hossza :.
Ha továbbra is növekszik, például számának megkétszerezése a sokszög oldalainak, a húrt például nagyjából megegyezik az ív hosszát, ami azt húzza.
Tehát, ha hajlamos a végtelenbe, a közelítés pontossága nő, a kerülete hajlamos egy bizonyos számú (jelöljük) van jelen, ezt a számot, és kerületének hosszával.
Esemény
Nézzük meg az eseményeket, amelyek előfordulnak (3.). Először is világosan megérteni, hogy minden rögzített, még a nagyon nagy, oldalsó hossza megfelel a hossza ív. És a sokszög kerülete kisebb, mint a kerülete. De nem egy konkrét szám, - egy változó, amely hajlamos a végtelenségig, de mi van, ha ez történik?
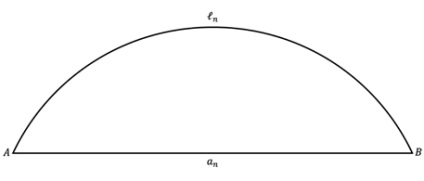
Ábra. 3. Részlet a kör, ahol - a hossza a megfelelő körív - oldalhosszúságú -gon
És van egy határ, hogy ez a tendencia? Ott! Ez a szám 0, de ez soha nem lehet elérni. Mi fog történni a jelen, de elfogadhatatlan limit, mikor? A és B pontok egybeesnek, sokszög egyesül a kerülete, kerülete kerülete értéket veszi fel, itt, ez az érték - kerülete.
Tétel: aránya kerületének és átmérőjének nem függ a kerülete, azaz ugyanezt bármely két kört.
Van két kört. ; ; és jellemzői az első kör:
Részletek a másik kör :.
Ezekből kapcsolatok megkapjuk; /
Ie a hossz aránya az átmérője nem függ a kerülete. Ez azt bizonyítja, a tétel.
Az arány a kerülete annak átmérője megegyezik, már megalapozott ismert képlet: /
Mi kifinomult a koncepció a kör és megalapozott képlet kerülete, megvitatták az elmélet viszonya kerületének és átmérőjének.