Dmitry Gusev - egy lenyűgöző logika - 40. oldal

93. Parrot élt legalább 100 éves, és csak válaszolni a kérdésekre „igen” vagy „nem”. Ahogy szüksége van kérdéseket feltenni, hogy megtudja, a kora?

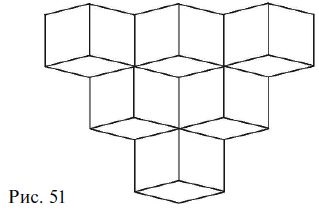
94. Hány kocka ábrán látható. 51?

95. Három borjú - hány lába?

96. Egy ember fogott fogságban, a következőket mondta: „Az én börtönben volt található, a felső részén a vár után napi munkájára voltam képes lebontani az egyik bár a keskeny ablak a lyuk lehet átjutni, de a távolság a talaj túl nagy volt, hogy .. csak ugorj le. az egyik sarokban a börtön találtam egy elfelejtett valaki kötelet. azonban ő túl rövid volt ahhoz, hogy menjen le rá. aztán eszembe jutott, egy bölcs meghosszabbított túl rövid neki egy takarót, levágta része alulról és varrni a tetején . Tehát siettem, hogy felére csökkentik a kötelet, majd kötni a két formált részből áll. Aztán lett elég hosszú, és én boldogan ment végig le. " Hogyan narrátor sikerül ezt?

97. A kérdező megkérdezi elképzelni olyan háromjegyű szám, majd felajánlja, hogy megírja a számok fordított sorrendben, hogy még egy háromjegyű szám. Például 528-825, 439-934, és így tovább. N. Aztán megkérdezi a több kevesebb, és közölni vele a különbség az utolsó számjegyet. Utána felhívta a különbséget. Hogy csinálja?

98. hét volt - talált hét rubelt. Ha nem hét, és három közülük mentek, sokan találtak meg?

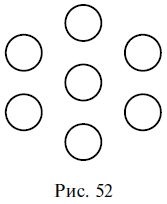
99. Osszuk a mintát a hét kört, három egyenes vonalak hét részre úgy, hogy minden egyes része volt egy kör (ábra. 52).

100. Globe karika húzta az egyenlítő mentén. Ezután csavarja a hossza növekedett 10 méter. Ahol felülete közötti a világon, és karika kialakítva egy kis rés. hogy a személy képes lesz átvészelni ezt az űrt? A hossza a Föld egyenlítő körülbelül 40.000 kilométert.

1. az első zsákot ki kell húzni egy érmét egy második - két, a harmadik - három, stb (a tizedik a táska - mind a 10 érme) ... Ezt követi egy ideje mérlegelni az összes érmét együtt. Ha köztük nem volt hamis érméket, t. E., akkor mind súlya 10 gramm, a teljes súlya 550 g. De ahogy között lemérjük érmék kovácsolt (11 gramm), a teljes súlya több mint 550 gramm. És, ha ő 551 gramm, a hamis érmék vannak az első zsákot, mert ez, vettünk egy érmét, ami adott egy extra gramm. Ha a teljes súlya 552 gramm, ez azt jelenti, hogy a hamis érmék vannak a második zsákot, mert ez, van két érmét. Ha a teljes súlya 553 g, majd, a hamis érmék a harmadik táska, és így tovább. D. így csak egy súlyozó lehet pontosan beállítani, a hamis érmék vannak jelen a zsákban.

2. Szükséges, hogy a cookie-k ki az üveget „zabliszt cookie” megjelölés (lehet bármilyen más). Mivel a bank van írva tévesen, akkor Shortcake vagy csokoládé. Tegyük fel, hogy van omlós. Ezt követően meg kell cserélni a label „zabliszt cookie” és „omlós”. És mivel a feltétele az összes címke összekeverednek, ez most a bankban a felirat: „A csokoládés sütemények” zabpehely, de a bank azt mondja: „zabliszt cookie” csokoládé, akkor meg kell cserélni két címke.

3. A szekrény kell, hogy csak három zokni. Lehetőség van mind a 4 változatban: három fehér zokni; három lábujj fekete; két zokni fehér, egy fekete; két zokni fekete, egy fehér. Minden ilyen kombinációk van egy megfelelő pár - fehér vagy fekete.

4. Az óra üt 12 órán át 66 másodpercig. Ha üt az óra 6 óra, az első 5 csap nyúlik ki, hogy az utolsó nyílásba. Interval 6 mp (1/5 30). Ha üt az óra 12 óra, az első löket az utolsó menetben 11 időközönként. Mivel a hossza a intervallum 6 másodpercig, majd ütni 12 óra 66 óra szükséges másodperc 11 · 6 = 66.

5. A tó lesz borított levelek liliom félig az 99. napon. Azzal a feltétellel, a levelek száma naponta megduplázódik, és ha a 99. napon a tó hatálya alá tartozó levelek felét, majd a következő nap, és a másik felét fogják fedezni tó liliom levelek, t. E. Teljesen borított tó 100 nap.

6. Az út telt az ötödik emeleten (4 span) személyszállító lift, kétszer az útnak a harmadik emeleten (2 járat) rakomány. Mivel az utas lift 2-szer gyorsabb, mint a rakomány, akkor lesz saját módon ugyanabban az időben.

7. Az létre kell hozni egy egyenletet megoldani ezt a problémát. Száma libák repülés - ez. „Most, ha volt, mint most (azaz x ..), - liba mondták -, és még annyi (azaz x ..), de még mindig fele annyi (azaz 1/2 ..), de egy másik negyed sok (azaz. e. 1/4), és még akkor (azaz. e. 1. lúd), ez az, amikor mi lett volna 100 liba. " A következő egyenletet:

Végezzük felül a bal oldalon az egyenlet:

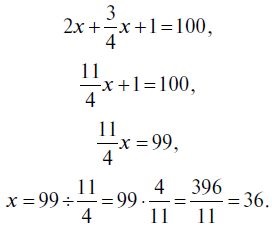
Tehát, egy nyáj liba volt 36.

8. A hiba abban rejlik, hogy az építési mindkét oldalán az egyenlet 2 = 2 négyzeten. Ez azt a látszatot kelti végre ugyanazt a műveletet (négyszögesítése) mindkét oldalán az egyenlőség valójában több mint minden része az egyenletnek, hogy különböző műveleteket hajtsanak végre, mert a bal oldali megszorozzuk 2-vel, és a jobb megszorozzuk 2.

9. Az az állítás, hogy a atommag kevesebb, mint 2-szer, természetesen nem igaz: valójában 10-12 cm-rel kisebb, mint 10 ~ 6 cm nem egy tényező 2, és egy millió alkalommal.

10. repülést „tartják” a levegőben, így repülni repülővel a hold nem lehet, mert a levegő a nyitott térben van.

11. A tűt acélból, és a réz érme. Acél sokkal nehezebb, mint a réz, ezért lehetséges, hogy szúrja értéket. Kézzel meg lehet csinálni. Ha azonban megpróbál pontszám egy tűt a kalapács érme, ez is nem működik: az éles tű végére terület olyan kicsi, hogy a hegye vibrál, csúszik a felületen az érme. Ahhoz, hogy egy tűt, hogy stabil, meg kell vezetni egy kalapáccsal egy érme keresztül egy darab szappant, viasz vagy fa, ez az anyag ad állandó és a tűt a helyes irányba, és ebben az esetben ez lesz szabadon áthaladhat a réz érme.

12. Az üveg lehet elhelyezni, több mint ezer csapokat. Ebben az esetben, egy csepp víz nem fog fordítani, de alkot egy kis dudor a vízüveg élek, a „hegy”. Szerint Archimedes törvény test vízbe merül, kiszorítja azt a víz térfogata egyenlő a térfogatának a szervezetben. A kötet egyik csap olyan kicsi, hogy a víz térfogata „diák” az üvegfelület a kötet több mint ezer csapokat.

13. A portré ábrázolja fia Ivanov. lehet, hogy egy egyszerű rendszer, hogy megoldja a problémát: