Meghatározása sebesség koordináta módszerrel
Az általunk használt (4) egyenletben, és vigye az idő származék
B (8) vannak nyúlványok a sebességvektor a koordináta-tengelyen, amikor az egység vektorok
A kiemelkedések a sebesség a koordinátatengelyeken definiáljuk, mint az első alkalommal származékok a megfelelő koordinátákat.
Ismerve a vetítés, megtalálja a vektoros egység és annak irányát
Sebességének meghatározása a természetes folyamatát
Adott egy pályája anyagi pont és a változás a görbe koordinátákat. Tételezzük fel kellett pontjában t1
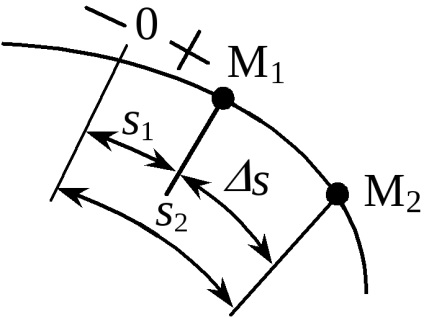
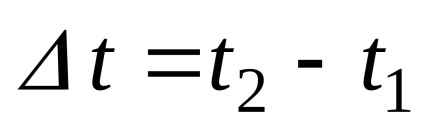
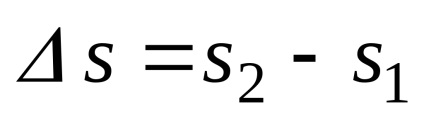
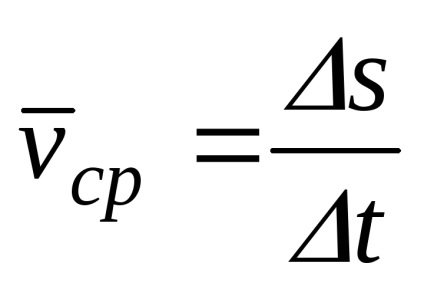
Ahhoz, hogy megtalálja a sebessége egy adott időben átadni határ
,
vektor sebessége egy pontot a természetes mozgását hozzárendelési módszer úgy definiáljuk, mint egy első idő-származékot a görbevonalú koordináta.
Az gyorsulása anyagi pont megérteni vektor mennyiség, amely jellemzi a változás mértéke a sebességvektor egy pont nagyságú és irányú idővel.
Gyorsítás pont, amikor mozgásvektor hozzárendelési folyamatot
Tekintsük a ponton két időpontban t1 (
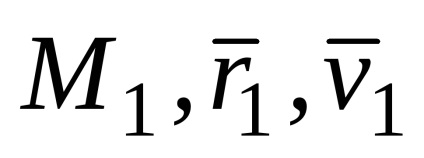
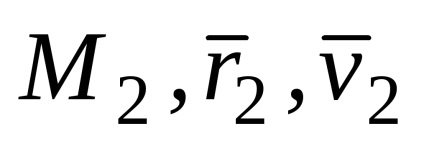
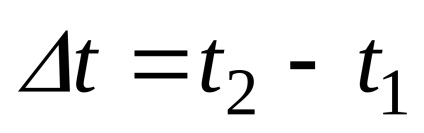
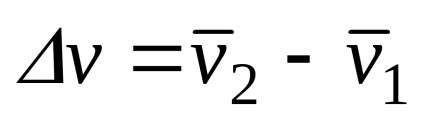
vektor

P
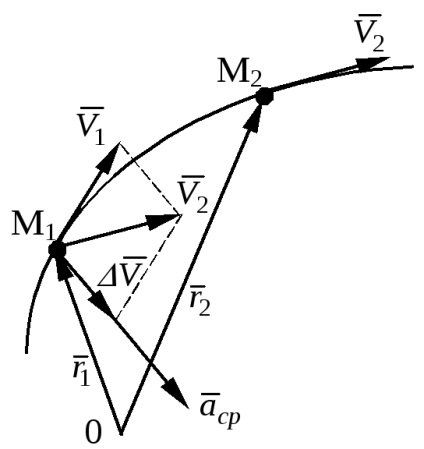
Ahhoz, hogy megtalálja a gyorsulás egy adott időpontban száll át a határt
,
egy adott időpontban a gyorsulás meghatározása a második deriváltja a sugár vektor egy pont, vagy az első származékot sebességvektor idővel.
Gyorsulásvektor található a simuló síkban felé irányuló, és a konkáv az útvonal.
Gyorsulás koordináta mozgáspontba hozzárendelési folyamatot
Az általunk használt vektor egyenlet kommunikációs módszerek és koordinálja a mozgást feladat
.
És vigye a második derivált
,
A (15) egyenletben a nyúlványok a gyorsulás vektor a koordináta-tengelyen, amikor az egység vektorok
Az előrejelzések gyorsítást a koordináta-tengelyek vannak meghatározva, mint az első alkalommal származékai a sebességet a nyúlványok vagy a második a származékok a megfelelő időt koordináták.
A nagyságát és irányát a gyorsulásvektor megtalálható az alábbi kifejezésekkel
A gyorsulás szempontjából a természetes mozgás feladat folyamat
P
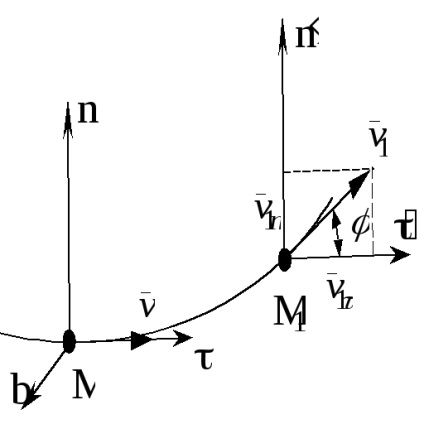
A gyorsulás ezután úgy határozzuk meg annak vetülete a tengelyen egy természetes koordináta-rendszer mozog az M pontban a tengelyek így irányított a következőképpen:
M - tangens, irányított mentén érintő a pályára a pozitív távolság referencia,
Mn - egy rendes lakás, mentén irányul normál fekvő simuló sík felé irányuló, és konkáv az út,
Mb - binormal merőleges síkban Mn és formák az első tengelye jobbkezes.
Mivel a gyorsulásvektor rejlik simuló sík, ab = 0. megtalálják a vetítés gyorsulásának a másik tengely.
Vetítjük (19) a koordinátatengelyeken
A ponton keresztül M1 tengely párhuzamos a tengely az M pont, és megtalálja a vetítési sebesség:
ahol - az úgynevezett szög szomszédossági.
Behelyettesítve (22) be (20)

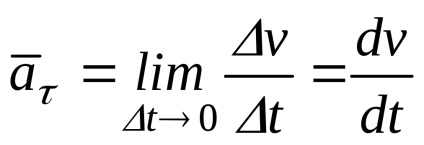
A tangenciális pont a gyorsulás által meghatározott első alkalommal származékot a sebesség vagy a második idő szerinti deriváltja a görbevonalú koordináta.
Tangenciális gyorsulás jellemzi a változás a sebességvektor nagyságát.
Behelyettesítve (22) be (21)
.
Mi szaporodnak a számláló és a nevező által s megismerni kívül
ahol
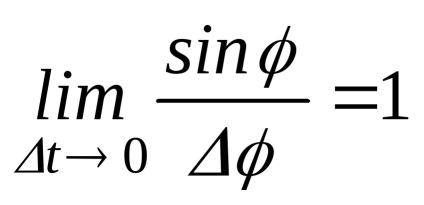
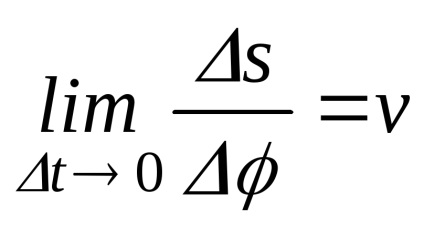
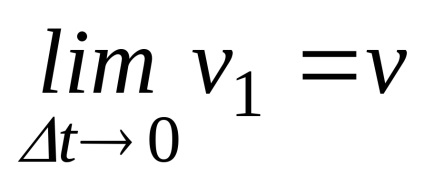
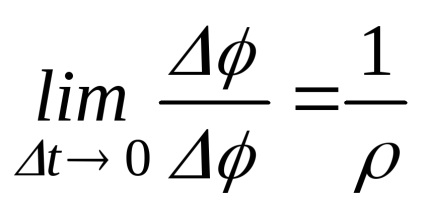
Behelyettesítve a kiszámított határértékeken (24), megkapjuk
Normál gyorsulás pont határozza meg az arány a sebesség négyzet a görbületi sugara az utat ezen a ponton.
Normál gyorsulás jellemzi a változása a sebesség vektor irányába, és mindig irányul a konkáv a pálya.
Végül megkapjuk vetülete gyorsulást az anyag pont a tengelyen egy természetes koordináta-rendszer, és egy vektorba egységet