Meghatározó a grafikon - előadás geometria
Leírás előadások az egyes diák:
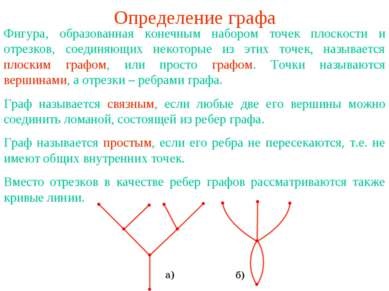
Meghatározó a grafikon alakja, amelyet egy véges ponthalmaz a síkon és a szegmensek összekötő néhány ilyen pont az úgynevezett síkbeli gráf, vagy egyszerűen számolni. A pontok nevezett csúcsok és - egy él. Graph úgynevezett csatlakoztatott, ha bármely két csúcsa lehet csatlakozott egy sokszögű sort, amely élek a gráf. A grafikon az úgynevezett egyszerű, ha a szélei nem metszi egymást, azaz, Nincs közös belső pontja. Ehelyett a szegmenseket gráf élei minősülnek görbe vonalak.
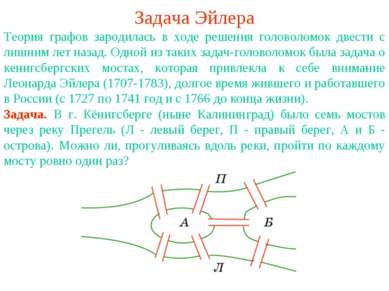
A probléma az Euler Gráfelmélet származott során rejtvények megoldása több mint kétszáz évvel ezelőtt. Az egyik ilyen probléma puzzle volt a probléma a Königsberg híd, amely felkeltette a Leonhard Euler (1707-1783), hosszú ideig élt és dolgozott Oroszországban (1727-1741 és 1766-től haláláig). Feladat. A város Königsberg (Kalinyingrád most) volt hét híd a folyó felett Pregel (L - bal parton, R - jobb partján, az A és B - A sziget). Lehet, séta a folyó mentén haladnak át minden híd pontosan egyszer?
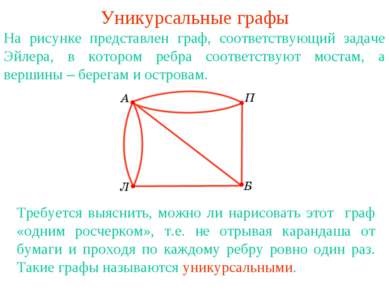
Unicursality grafikonok ábrán a grafikon megfelelő Euler, ahol is az élek megfelelnek a hidak, és a csúcsokat - a partján, és a szigetek. Ez szükséges annak megállapítására, hogy lehetséges-e, hogy felhívja a grafikont „egy csapásra”, azaz felemelése nélkül ceruzát a papírról és átmegy minden élét pontosan egyszer. Az ilyen grafikonok nevezzük unicursal.

Tétel vertex index az a szám élek konvergáló ebben vertex (bordák, kezdő és befejező kétszer számolni a felső). Tétel. Unicursal grafikon a csúcsok száma páratlan index értéke nulla vagy kettő. Bizonyítás. Ha a gráf unikursalen, akkor van eleje és vége bypass. A maradék csúcsok még indexet, mivel minden egyes bejegyzés egy csúcsot, és a kimenet. Ha az elején és a végén nem ugyanaz, ez az egyetlen csúcsot páratlan index. Az elején a kimenetek eggyel nagyobb, mint a bemenet, és a végén a bejegyzések egy több, mint a teljesítmény. Ha a start egybeesik a végén a csúcsok páratlan index nélkül. Ennek a fordítottja is igaz: ha egy gráf csúcsainak számát páratlan index értéke nulla vagy kettő, akkor unicursal.

Megoldás az Euler megoldása Euler probléma. Találunk az indexek csúcsok az Euler probléma. Vertex A-nak egy index 5, B - 3, n - 3 és N - 3. Így van négy csúcsa páratlan indexű, és ezért ez a grafikon nem unicursal. Tehát lehetetlen csak egyszer halad át mind a hét hidak.

1. kérdés Melyik szám az úgynevezett grafikon? A: A grafikon egy alak által alkotott véges ponthalmaz a síkban és a szegmensek összekötő néhány ilyen pont.

2. kérdés Melyik grafikon nevezzük unicursal? Válasz: A grafikon az úgynevezett unicursal, ha lehetséges, hogy dolgozzon egy „egyetlen csapással”, azaz felemelése nélkül ceruzát a papírról és átmegy minden élét pontosan egyszer.

3. kérdés Mi a neve az index a csúcsok? A: Az index az a szám, a gráf élek, amelyek összetartanak a csúcsa (bordák, kezdő és befejező kétszer számolni a felső).

4. kérdés Mit mondhatnék a vertex indexek unicursal grafikonon? Válasz: unicursal gróf a csúcsok száma páratlan index értéke nulla vagy kettő.
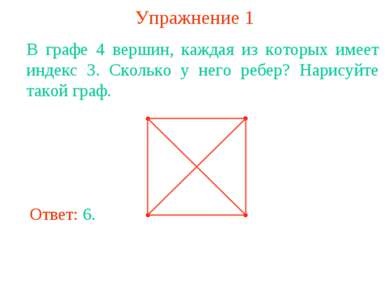
1. gyakorlat A 4. oszlopban csúcsok, amelyek mindegyike egy index 3. Hány bordák ez? Rajzolj egy gráf.
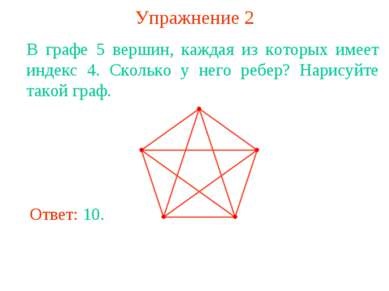
2. gyakorlat 5. oszlop csúcsok, amelyek mindegyike egy index 4. Hogyan volt a bordák? Rajzolj egy gráf.
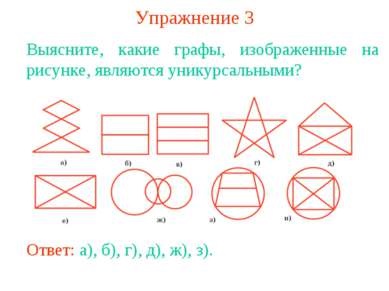
3. gyakorlat megtudja, mi a grafikon az ábrán látható a unicursal? Válasz: a), b), d), e), g), h).

4. gyakorlat tud számolni kell: a) egyik csúcsa páratlan index; b) két csúcsa páratlan indexű; c) a három csúcsa páratlan indexű; d) négy csúcsa páratlan indexű? Válasz: a), c) nincs; b), d) és.
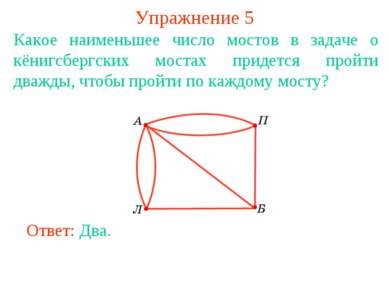
5. gyakorlat Mi az a legkisebb hidak száma a probléma a königsbergi hidak menni kétszer megy át minden híd? Válasz: Két.
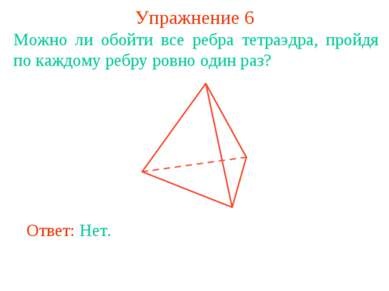
6. gyakorlat Kaphatok körül a szélei tetraéder, áthalad minden él pontosan egyszer? Válasz: Nem
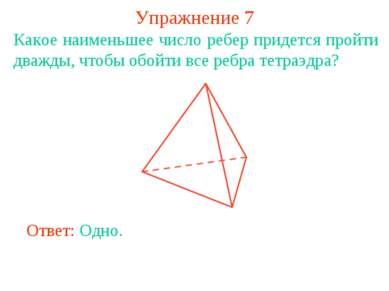
7. feladat Mi az a legkisebb számú élek kell menni kétszer kap körül a szélei tetraéder? Válasz: Egy.

8. gyakorlat Mi az a legkisebb számú élek már itt kétszer kap körül a szélei tetraéder, és visszatér a kiindulási csúcsból? Válasz: Két.
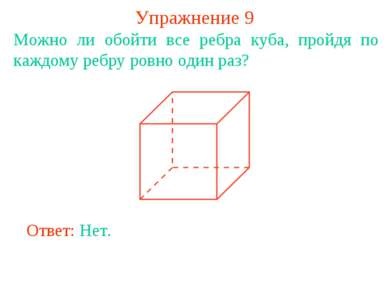
9. gyakorlat Kaphatok szélek körül a kocka kattintva minden szélén pontosan egyszer? Válasz: Nem
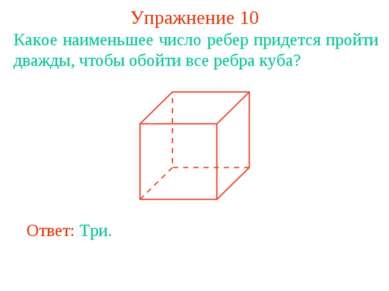
10. gyakorlat Mi az a legkisebb számú élek kell menni kétszer kap körül a széleit a kocka? Válasz: Három.
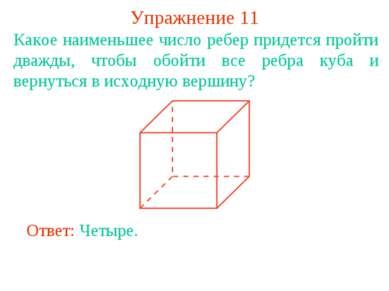
11. gyakorlat Mi az a legkisebb számú élek kell menni kétszer kap körül a széleit a kocka, és visszatér a kiindulási csúcsból? Válasz: Négy.
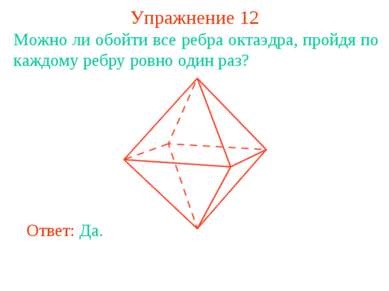
12. gyakorlat Lehetséges, hogy kb minden szélei oktaéder, áthalad minden él pontosan egyszer? Válasz: Igen.

Gyakorlat 13 Lehetséges, hogy kb minden szélei ikozaéder, áthalad minden él pontosan egyszer? Válasz: Nem

14. gyakorlat Mi az a legkisebb számú élek kell menni kétszer kap körül a szélei ikozaéder? Válasz: Öt.

15. gyakorlat Mi az a legkisebb számú élek kell menni kétszer kap körül a szélei ikozaéder, és visszatér a kiindulási csúcsból? Válasz: Hat.
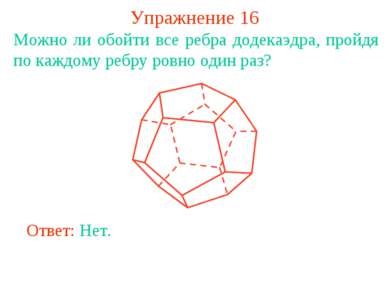
16. gyakorlat Lehetséges, hogy kb minden szélei a dodekaéder, áthalad minden él pontosan egyszer? Válasz: Nem
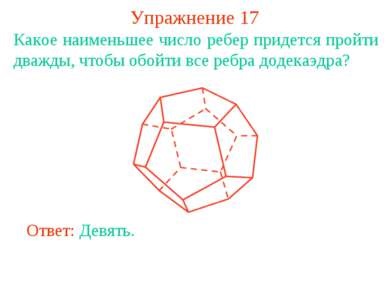
17. gyakorlat Mi az a legkisebb számú élek kell menni kétszer kap körül a széleit a dodekaéder? Válasz: Kilenc.
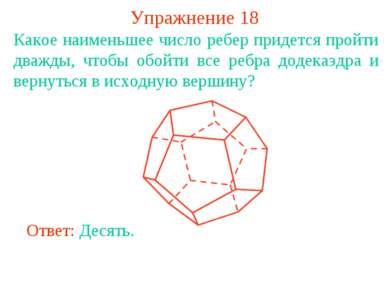
Gyakorlat 18 Mi az a legkisebb számú élek kell menni kétszer kap körül a széleit a dodekaéder és visszatér a kiindulási csúcsból? Válasz: Ten.
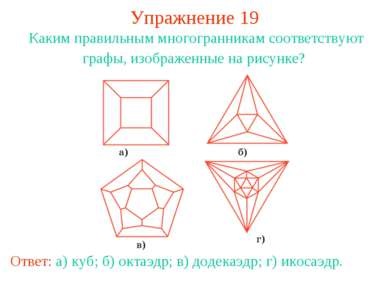
19. gyakorlat Hogyan szabályos poliéderek megfelelő grafikon az ábrán látható? Válasz: a) a kocka; b) az oktaéder; AT) dodekaéder; g) ikozaéder.
Kapcsolódó bemutatása

Portfolió modell és fotós

Az állatok azonosítása és a madarak városrészek Hani falu, élőhelyeik függően természetes - éghajlati domborzati

Meghatározása jódtartalma élelmiszerek

Meghatározása csúszó súrlódás

Mennyiségi meghatározása A C-vitamin az élelmiszerekben jodometriás módszerrel

Meghatározó szerepe a kutya a történelem az emberi társadalom és annak megítélése a különböző etnikai és kulturális hagyományok

Grafikonok. A mértéke csúcs. Megszámoljuk a szélek

Önrendelkezésének diákok középiskolában a jövőben szakma
7311 7866 7998 9579 9630 9867 10685 11581
Előadások a geometria lecke

Szinusz, koszinusz, tangens a 9. évfolyam

jelek egy paralelogramma

Symmetry - körülöttünk

a probléma a felvételi vizsgák


Geometriai konstrukciók vonalzóval és iránytű


„Valószínűsége”


polyhedra

axiális és központi szimmetria

Nézni az összes geometria a prezentáció
32685 32738 32752 32898 32920 33141 33503 33504 33522 33751 33939 34145