Az alakja egy parabola, az egyenlet a parabola, a tengely és a paraméter a parabola, az érintő a parabola és annak tetején

Az alakzat egy parabola. Az egyenlet a parabola. A parabola egyedileg határozza meg a fókusz F és direktrixszel f. Merőleges x ≡ FD. csökkent a fókuszt direktrixét, az úgynevezett a tengelye a parabola, és p a távolság a hangsúly a direktrix - annak a paraméter (lásd 1. ábra ..).

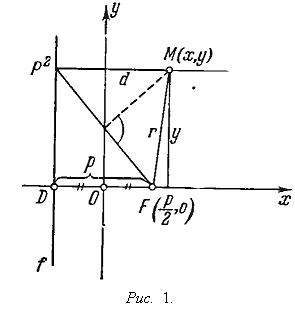
A meghatározás a parabola a pontok helye egyenlő távolságra F és f. Ebből következik, hogy a parabola szimmetrikus a saját tengelye körül. ahol az x tengely a parabola csak egy közös pont O - középső szegmenst FD. O pont az úgynevezett csúcsa a parabola.

Keresztül az O pont az y vonal. merőleges az x tengelyre. Nyilvánvaló, kivéve az O pont a vonalon y más pontok a parabola, t. K. Minden P pontot az Y vonal. O. eltér a r távolságtól a fókusztávolság nagyobb távolságra PP1 = d egyenlő direktrixét, és így, R. d> 1, v. e. a P pont tartozik parabola. Minden P pont sík a fókuszpont F található ellentétes oldalán direktrixét, R> d. és ezért ebben a felében a parabola mutat ott. Következésképpen, az a pont a parabola oldalán található az Y vonal. amely a hangsúly a parabola. Szimmetria, bármely párhuzamos egyenes vonal y és amelynek a parabola egy közös pont, azt, és a másik a közös pont és egy egyenes y van egy közös pontja a parabola. Ennek eredményeként, a vonal y nevezzük érintő a parabola a tetején.

Most vállalja a parabola x az x tengelyen van a tengelyen, és a tangens y a csúcson - az y tengely derékszögű koordináta rendszerben. Legyen M (x y.) - tetszőleges pontja a parabola (lásd 1. ábra ..). majd

és a következő egyenletből: R 2 = d 2, hogy

Az alakja egy parabola, az egyenlet a parabola, a tengely és a paraméter a parabola, az érintő a parabola, pontjainak.