mérnöki mechanika
3. Lapos rendszer véletlenszerűen elhelyezett erők
Ható erő egy teljesen tömör testű, akkor nincs hatása változó, párhuzamosan mozognak magát bármely testrész, hozzátéve ugyanakkor egy pár pillanatban egyenlő a pillanatot hordozható energiát képest a pont, ahol az erő átvitele (ábra. 10).
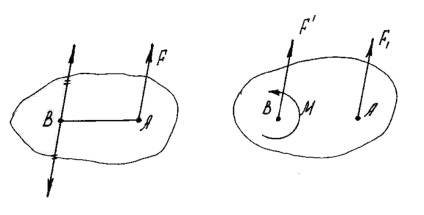
Minden síkja rendszer ható erők egy merev test, ha aktivált egy tetszőlegesen kiválasztott központ O helyettesíti egy erő R. egyenlő fő vektor rendszer és alkalmazott, hogy a középső O. és egy pár a MO nyomatékkal. egyenlő a fő pontja a rendszer középpontjához viszonyítva O (ábra. 11).
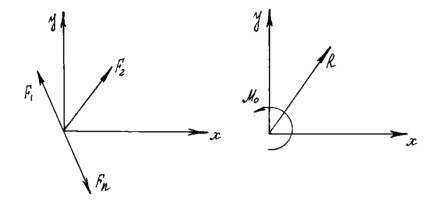
Különös esetekben hozza lapos rendszert erők a legegyszerűbb formában:
- Ha ez a rendszer erők R = 0, és ME = 0, akkor az egyensúlyi;
- Ha ez a rendszer R erőket ≠ 0, M = 0, akkor hozzuk kapott.
Az alapvető formája az egyensúlyi körülmények között. szükséges és elégséges feltétele az egyensúly egy tetszőleges sík rendszert erők összege az előrejelzések minden erő mind a két tengely és összegével pillanatok kapcsolatos bármely központ síkjában fekvő erőinek nulla.
A második forma az egyensúlyi körülmények között. Az egyensúly egy tetszőleges sík erőrendszer szükséges és elégséges, hogy az összeg a pillanatok ezek az erők mintegy két pont A és B összegével előrejelzéseket az x tengelyen. nem merőleges az AB egyenes. Ez volt nulla.
A harmadik forma az egyensúlyi körülmények között. Az egyensúly egy tetszőleges sík erőrendszer szükséges és elégséges, hogy az összeg a pillanatok ezek az erők bármilyen három központ A. VS nem fekszenek egy egyenes vonal, ez egyenlő a nullával.
4. A koncepció egy farmon. kiszámítása gazdaságok
Fermoy úgynevezett merev szerkezete egyenes vonalú rúd csuklók kapcsolják össze a végein (12.).
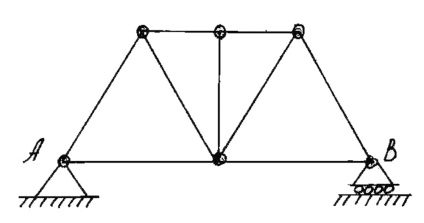
Ha az összes vonal gazdaságok fekszenek ugyanabban a síkban, a farm hívják lapos.
A csomópont rudak mezőgazdasági úgynevezett csomópontok.
Ferde rudak nevezzük fogszabályozó. függőleges - oszlopok.
A távolság a két láb között nevezzük span.
Farms számítást végezzük két módszer:
1) A módszer vágó egység. ami csökkenti a soros venni az egyensúlyi állapotok erők konvergáló az egyes gazdaságokban csomópont;
2) módszer szakaszok (Ritter-módszer), amely áll az a tény, hogy a mezőgazdasági két részre van osztva része-szakasz áthalad a három rúd, amelyben a szükséges erő meghatározásához, hogy egyensúlyi egyenlettel.
5. A térbeli erő rendszer
Abban a pillanatban, az erő, ami a tengely nevezzük skaláris érték megegyezik a pillanatban ennek az erőnek a vetítési sík merőleges a tengelyre vett képest a tengely metszéspontja a géppel.
Találni egy pillanatra az erő, ami a Z tengely (. 13. ábra), akkor:
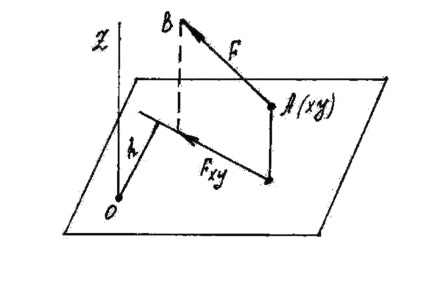
1) xy síkra. merőleges a z-tengely;
2) tervezzen egy F erő a gépen, és értékének kiszámításához Fxy;
3) csökkentette a az O pont a metszéspontja egy merőleges síkban irányára Fxy H és annak hossza;
5) meghatározzuk a jel pont.
Különleges esetekben, amikor meghatározzák a pillanat:
1) Ha egy erő, a tengellyel párhuzamos, a pillanatban a tengely körül nullával egyenlő, mivel a Fxy = 0;
2) Ha az erő hatóirányának metszi a tengelyt, a pillanatban a tengely körül is nulla, mivel a h = 0;
3) Ha az erő merőleges a tengelyre, a pillanatban a tengely termék az erő modul közötti távolság az erő és a tengely.
A egyensúlyi körülmények között tetszőleges térbeli rendszer erők. Az egyensúly egy tetszőleges térbeli rendszer erők szükséges és elégséges, hogy az összeg a nyúlványok az összes erők mind a három tengely és összegével pillanatok tekintetében ezek a tengelyek minden nullával egyenlő.
II. Kinematika és szilárd
1. Alapvető fogalmak kinematikai
1.1. Módszerek meghatározva a pont mozgásának
Úgynevezett kinematikai ága a mechanika, hogy tanulmányozza a geometriai tulajdonságok a mozgás szervei, függetlenül azok tehetetlenségi (tömeg), és a ható erők.
Filmszerűen meg a mozgást vagy a törvény a test mozgása (pont), majd állítsa be a testhelyzet (pont) képest egy adott referencia-rendszer bármikor.
Referencia rendszer az úgynevezett valós vagy szuszpendált szilárd, amelyekkel kapcsolatban határozza meg, az egyéb mozgatható testek.
A természetes módon meghatározni mozgás. Folytonos vonal, amely leírja a mozgó pontra vonatkoztatva ez a referencia rendszer, az úgynevezett pályája pont. Ha az elérési út egy egyenes vonal, a mozgás pontot nevezzük egyenes, és ha a görbe - ívelt.
A törvény a mozgás pályája mentén pont által kifejezett S = f (t).
Annak beállításához, a mozgását egy pont, amely természetes módon, meg kell tudni:
1) a pálya pont;
2) a referencia pontot a pályája jelezve a pozitív és negatív irányban referencia;
3) A törvény a mozgás pályája mentén pont a S = f (t).
A számérték pont sebessége ebben az időben az első származék távolságban tartja időpontban:
A számértéke gyorsulás pont egy adott időpontban egyenlő egy első deriváltjának a sebesség:
Koordinátor kétirányú forgalom hozzárendelés
Törvény a mozgás a pont a koordináta módszerrel fejezi ki az egyenleteket:
A kiemelkedések a sebesség a koordinátatengelyeken egyenlő, ami első derivált a megfelelő pontok koordinátáinak az idő:
Az előrejelzések a koordináta-tengelyen gyorsulás egyenlő az első származékot a sebessége a nyúlványok vagy a második származékot a megfelelő pontok koordinátáinak az idő.
1.2. Tangenciális és normális gyorsítás pont
A vetítés a gyorsulás pont egy érintőleges röppályája úgynevezett tangens vagy érintőleges uskoreniema τ.
A vetítés a normál gyorsulás az úgynevezett normális uskoreniema τ.
Tangenciális és a normál gyorsulás (ábra. 14) nem tekinthető vetítés, hanem mint komponensek teljes gyorsulás. t. e. vektorként mennyiségét és a teljes gyorsulás egyenlő
A tangenciális komponens érintőleges, valamint a sebességvektor V., és ezért nem befolyásolja az irányt a sebesség, de hatással az értékét.
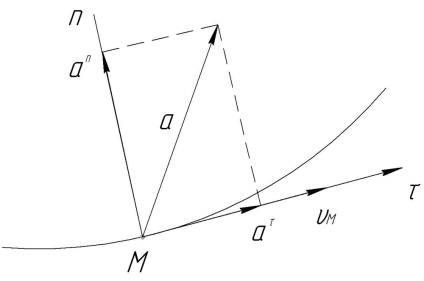
A normál komponens merőleges a sebességvektor, és ezért nem befolyásolja a értéke a sebességet, de a hatása annak irányát.
, ahol ρ - görbületi sugár.
2. A transzlációs és rotációs mozgást egy szilárd
Progresszív egy mozgása egy merev test, amelynek során bármely húzott egyenes vonaltól a szervezetben mozgatjuk, míg a fennmaradó önmagával párhuzamosan.
Előrehaladó mozgása során a valamennyi pontokat a test mentén egyenlő (egybeesése kérelemre), és van egy útvonal minden egyes alkalommal ugyanaz a nagysága és iránya a sebesség és a gyorsulás.
Során előre közös az összes pontokat a test sebessége V hívás aránya transzlációs mozgás a szervezetben. és gyorsulását - gyorsulás transzlációs mozgás.
Forgási mozgás úgynevezett szilárd test, amelyben bármely két pont tartozó a test (vagy változatlanul társítva) maradnak az egész mozgás rögzített.
A átmenő két fix pont, az úgynevezett a forgástengely.
Az egyenlet γ = f (t) jelenti a törvény a forgó mozgás egy merev test. ahol γ - elfordulási szögét a szervezetben.
A fő kinematikai jellemzői a forgó mozgás a szilárd test a szögsebesség és szöggyorsulással ω ε.
A szögsebesség a test egy adott időben számszerűen egyenlő az első származékot a forgásszög idővel:
A szöggyorsulás a test egy adott időpontban számszerűen egyenlő az első származékot szögsebesség vagy a második származékot a forgásszög a szervezet idővel:
Ha a modul szögsebesség idővel növekszik, a test forgását az úgynevezett gyorsított. és ha csökken - késik.
Ha a szögsebesség egy test marad állandó mozgásban egész idő (ω = const), a forgó test nevezzük egységes.
Ha a szöggyorsulás a test egész mozgást folyamatosan (ε = const), az elforgatás nevezzük ravnoperemennym.
A lineáris sebesség a v pont egy forgó merev test számszerűen egyenlő a termék a szögsebesség ω a test R távköznyire ettől a ponttól a forgástengely.
A lineáris sebesség érintőleges a által leírt kört pont vagy merőleges a síkra, amely áthalad a forgástengely.
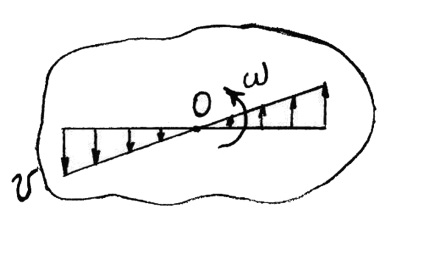
Mivel az összes pontokat a test szögsebessége ω jelenleg ugyanaz az érték, akkor ebből az következik, hogy a lineáris sebessége a forgó test pontok arányos a távolságok a forgástengely (ábra. 15).
A tangens uskoreniea τ irányul érintőlegesen a röppálya (a mozgási irányt, mikor a test sebességgel forgatni, vagy az ellenkező irányba, ha a test el van forgatva túl lassan); gyorsulási mező mindig sugárirányban a forgástengely R (ábra. 16).
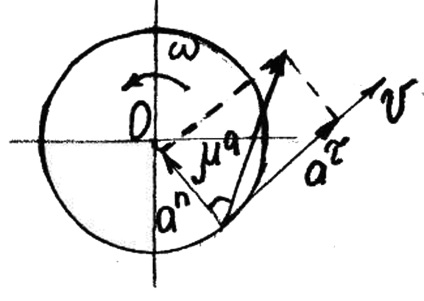
Teljes gyorsulás pont megegyezik az a = R.
Eltérés teljes gyorsulásvektor a kör sugara által leírt a pontot határozza meg a szög μ, amelynek kiszámítása a következő képlettel: