Lineáris programozás munkaprogram, vizsgálati papírokat, valamint a tankönyv, 3. oldal
Behelyettesítve a koordinátáit a C pont (6; 5) az objektív függvényben megkapjuk a megoldást a problémára:
.

1.5. konvex halmazok
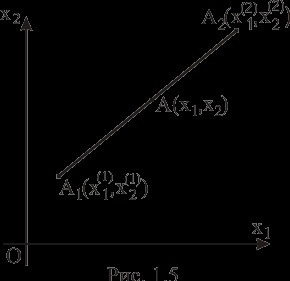
kollineáris, hol és
, , .
Tekintettel arra, hogy a (5.12), a pont koordinátái A a pontok koordinátáinak hasonló mennyiségű és megszorozzák rendre, végül megkapjuk
Meghatározása 1.10.TochkaAyavlyaetsya konvex kombinációja pontokat, és amennyiben a feltételek teljesülnek rá (1,13).
Meghatározása 1.11.V Általában tochkaAyavlyaetsya konvex kombinációja pont, ha a feltételek teljesülnek rá
Meghatározása 1.12.Mnozhestvo úgynevezett konvex, ha tartalmaz egy konvex kombinációja bármely pont.
Geometriailag, ez azt jelenti, hogy ha két pont tartozik a készlet, és a szegmens ezeket összekötő pontokat tartozik ebbe a körbe.
Példák konvex halmazok vannak vágva, egy fél sokszög, kör, fél-kocka és mtsai.
Meghatározása 1.13.Tochka úgynevezett határról, ha szomszédságában ezt a pontot tartalmaz pontok tartozó set, és pont nem tartozik a készülékhez.
Meghatározása 1.14.Mnozhestvo úgynevezett zárt, ha tartalmazza az összes határ pont.
Meghatározása 1.15.Mnozhestvo úgynevezett korlátozott, ha úgy, hogy a labda radiusomRs központ bármely pontján a készlet tartalmaz egy sor teljesen.
Meghatározása 1.16.Uglovoy konvex beállítási pont egy pont, amely nem konvex kombinációja bármely a több különböző pontokat.
A beállított tetszőleges számú sarkok, egy (ábra 1.6a.), Két (ábra 1.6, b.), Három (1.6 ábra a.) Stb és végtelen számú szögletes pontot (ábra. 1,6 g).
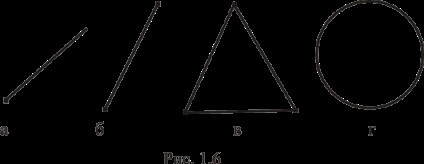
A szett nem lehet sarokpontok, például egyenes, fél-és stb
Meghatározása 1.17.Mnogogrannikom úgynevezett konvex, zárt, korlátos halmaz véges számú szögletes pont.
1.6. Tulajdonságok Az oldatok
Tétel alábbi 1.2-1.5 tulajdonságainak meghatározásához a megvalósítható sor megoldást, és a célfüggvény a sor megengedett terveket.
1.2 Tétel. A készlet elfogadhatónak probléma (1,15), (1,16) egy konvex halmaz.
1.3 Tétel. A célfüggvény a probléma (1,15), (1,16) eléri extrémuma a sarokban a beállított megvalósítható terveket. Ha az objektív függvény eléri extrémuma több sarokpontok, akkor eléri extrémuma konvex lineáris kombinációja bármelyik ezeket a pontokat.
,... - vektorok a feltételeket, akkor a rendszer a korlátok (1,16) a vektor jelöléssel:
Tétel 1.4. Ha a feltételek a rendszer vektorok lineárisan független, és úgy, hogy
,
ahol a - szögpontja a beállított határértékek az oldatok.
Tétel 1.5. Ha - a szögletes pont a korlátai az oldatok, a biztonsági rendszer megfelelő vektorok pozitív koordinátákat, lineárisan független.
Meghatározása 1.18.Opornym terv (határozat) egy lineáris programozási probléma az úgynevezett érvényes terv, amelynek feltételei a megfelelő vektorok pozitív koordinátáit, lineárisan függetlenek.
Tételek 1,4 és 1,5, ebből következik, hogy a szögletes beállított határértékek az oldatok referenciasíkot.
Meghatározása 1.19.Esli nulla koordináta referencia PLANAM, a terv az úgynevezett nem-degenerált ha menshem- degenerált.
Meghatározása 1.20.Bazisom támogatási nevű program feltételei vektorok alapján a rendszer, amely vektorok megfelel egy nem nulla koordinátákat a támogatási program.
A fenti tételek 1,2-1,5 hogy az optimális megoldás a lineáris programozás (1,15) (1,16) kell törekedni között sarokpontjait a beállított megvalósítható terveket. Ebben a tekintetben a következő kérdések merülnek fel:
- hogyan lehet megtalálni az eredeti terv?
- hogyan kell mozgatni a kezdeti támogatási program az új (egy sarokpont megoldásokat poliéder a másikra)?
- hogyan értékeli a változás a célfüggvény az átállás során egy hivatkozás egy másik tervet?
- hogyan kell meghatározni a vége a folyamatnak a válogatás a sarokpontok: vagy azért, mert az optimális megoldás, vagy azért, mert egy ilyen megoldás nem létezik, azaz Milyen feltételei vannak a optimalitásával a támogatási program?
A válaszok ezekre a kérdésekre adott az alábbi 1.7 pontban.
1.7. Építőipari alaptérképek
A folyamat építésének kezdeti támogatási program, az azt követő átmenet egy új (jobb) támogató program, gondoljunk csak a LP probléma öt változó és három egyenletet egy korlátos rendszerben. Az első szakaszban, akkor feltételezzük, hogy minden egyes egyenletet a rendszer a megszorítások, és csak ez tartalmaz egy változó arányban.
1.7.1.Postroenie kezdeti támogatási program
Nézzük meg a problémát
A rendszer egyenletek (1,19) tartalmaz három egység vektorok
, , .
Ezek képezik az alapját a rendszer vektorok ,,,,.
Összhangban az általános rendszerének bizonytalan lineáris rendszermegoldásoknál állapítsa változók, alapvető, és - a szabad és hinni. Ezután Slough (1,19) a következő alakú:
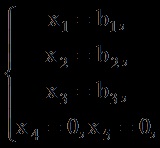
és a döntést a Slough egy vektor. A kapott terv lesz érvényes fel pozitív koordináták megfelelnek lineárisan független vektorok és
.
Beépített kezdeti támogatás a program biztosítja a célfüggvény értéke
.
Vegyünk egy konkrét példát
1.4 példa. Oldjuk meg az LP probléma.
1. Válassza a Start támogatási program
A beállított megengedhető feladatok tervek meghatározott lineáris egyenletrendszer (1,21). Ez a rendszer átírható vektor formában,