Beépített eljárások juhar

Ezután az interpolációs folyamatot hívhatja meg a fenti listák paraméterekkel történő megadásával, és ezen felül az interpolációs változónak az elfogadásával.

Érdemes megjegyezni, hogy az interp () eljárás eredménye egy kifejezés, nem operátor, ugyanúgy, mint az interpolációs Lagrange polinom létrehozásának eljárása során.

Egy másik népszerű interpolációs módszer a következő. A szomszédos csomópontok közötti minden intervallumban az interpolált függvény polinomiaként jelenik meg. De ellentétben mondjuk a Lagrange interpoláció, ahol ugyanazt a polinomot felhasználva szinte az összes pontot, ebben az esetben az egyes intervallumok polinom saját. Továbbá egyenlőség interpolációs függvény a csomópontok a táblázatba foglalt értékek interpolált funkció szuperponálódik az első, még és származékai folytonosságát állapotától érdekében, eggyel kevesebb, mint a mértéke interpolációs polinomok. Hasonló típusú interpolációt neveznek spline interpolációnak vagy spline interpolációnak. A legnépszerűbb a köbös spline-ek interpolációja.

Maple-ben a spline () a spline interpoláció végrehajtására használható. Az eljárásnak három kötelező paramétere van. Az első kettő a csomópontokkal és funkcionális értékekkel rendelkező listák. A harmadik paraméter az interpolációs változót adja meg. Ha a negyedik opcionális paraméter nincs megadva, akkor az interpolációt cubic spline-kkel kell végrehajtani, azaz. A csomóponti pontok "öltéséhez" a harmadik fokú polinomokat használjuk. Például, ha az eljárás paraméterei a korábban megvizsgált listákat határozzák meg, a funkció értékét a csomóponthoz viszonyítva adjuk meg, akkor ezt az eredményt kapjuk.

A spline () eljárás negyedik paramétere lehet egy lineáris, kvadratikus, köbös, kvartikus, interpolációs polinom. És az 1-től 4-ig terjedő szám jelzése megegyezik a felsorolt ​​szöveges opciók használatával, a fenti sorrend szerint.

Figyelem!
A negyedik paraméterként bármely pozitív egész szám megadható, nem csak az 1-től 4-ig terjedő tartományban. Csak ezeknél a számoknál van egy alternatív hívás a szöveges opción keresztül. Például a spline (X, Y, x, 5) segítségével a fentiekben leírt függvényt ötödik fokú polinomokkal interpolálhatjuk, és így tovább.

Az azonos funkciójú negyedik fokú polinomok interpolációja a következő.

Az kifejezések meglehetősen nehézkesek. Lássuk, mi történik, ha lineáris függőséget használunk spline polinomokként.

Az előző esethez képest egyszerűbb eredményt kapunk. Az egyszerűség azonban nem mindig jelenti a hatékonyságot. Ezt könnyű látni, ha grafikonokat állít elő a spline interpolációhoz különböző fokú polinomok segítségével kapott interpolációs függvényekhez.

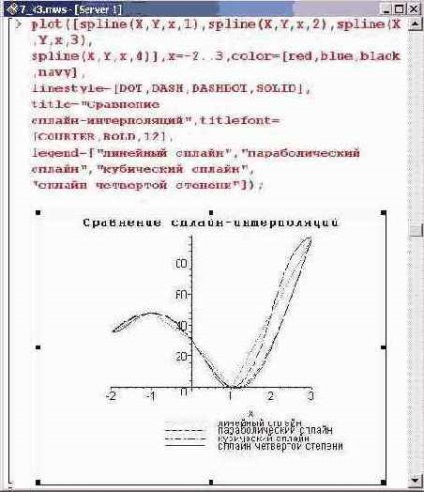
Nyilvánvaló, hogy a lineáris spline interpoláció meglehetősen durva. Ez nagyjából egyszerűen az interpolációs pontok vonalas kapcsolata. Ezt az interpolációs típust nagyon ritkán alkalmazzák. Ami az egyéb fok a polinomok kezdve a második, az előző jelentős különbség van köztük (legalábbis ebben a példában) nincs jelen. Azonban nem szabad megfeledkeznünk arról, hogy a spline polinomok mértéke meghatározza a kapott görbék simaságát. Ez különösen fontos abban az esetben, ha az interpolációból származó származékokat kell alkalmazni. Ebben az értelemben a polinom-interpoláció képest spline interpoláció az az előnye, hogy az interpolációs polinom és származékai egyedileg funkciók folyamatos és zökkenőmentes. Ezért érdekes a polinom interpoláció és a spline interpoláció eredményeinek összehasonlítása. Ehhez a megfelelő interpolációs függvények grafikonjait készítjük.

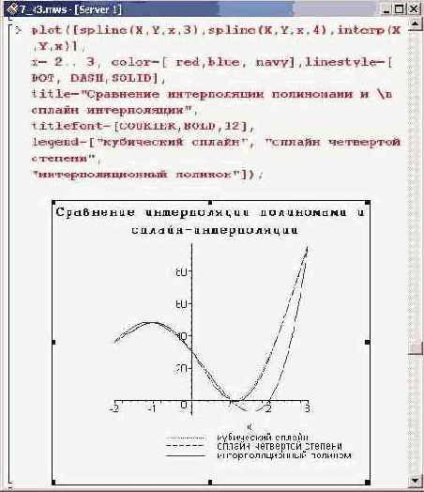
Látható, hogy mind a három grafika (spline a harmadik és a negyedik fokozat és a negyedik fokos polinom interpoláció) gyakorlatilag ugyanaz, főleg a bal oldalon az ábra. Igaz, az interpolációs polinom egy simább funkció, mint az első két. Amikor etrm az olvasó, hogy miért az interpolációs polinom foka egyenlő négy, nem esik egybe a spline függvény alapján szerkesztett negyedik polinomot? A választ olyan körülmények között kell keresni, amelyekből meghatározzák a spline funkciót. Így, amikor a spline interpolációt m + 1 pontú m polinomokkal végezzük, n spline polinomokat veszünk fel. Ezeken a polinomok kell aránya határozza meg a t + 1, és csak így azt kapjuk, n (m + 1) ismeretlen tényezők. Az interpolációs függvény egyenlõsége a csomóponton a táblázatban megadott értékekhez n + 1 feltételeket ad az ismeretlen koefficienseknek. Ezen túlmenően, a belső csomópontok (van n-1) feltételezzük folytonosság a származékok érdekében m-1, befogadó, amely együtt a folytonosság a funkciót, (n-l + (m-l) (n-l)) = m (n-l) körülmények között. Így a n (m + l) ismeretlen együtthatók egymásra (m (n-l) + (n + l)) = (n (m + l) - (m-l)) körülmények között. Ez persze nem elég - még mindig vannak m-1 feltételek. Rendszerint úgy kapják meg, hogy a vezető folyamatos származékok megfelelő számát megszüntetik az interpolációs régió határain. Ez az ún. Természetes választás további feltételekről. Elméletileg, matematikai szempontból tetszőlegesen választhatók, a megoldandó probléma függvényében. Ezeket a körülményeket különösen úgy lehet megválasztani, hogy az n fokú spline-ekkel történő interpoláció során az eredmény a Lagrange-interpolációs polinom.