A származékot és a differenciál a koncepció a származékos

Geometriai értelmében a származék 1

Fizikai és gazdasági értelmében a származék 2

Differenciálhatósága 3

A rendszer számítási a származék 5

Az alapvető szabályok differenciálás 5

Származékai alapvető elemi függvények 6

Magasabb származékok 7

Rugalmassága funkciója 8

Alapvető tételek a differenciálható függvények és alkalmazásaik 9

Szélsőséges funkciók 13

Konvexitása 16

Aszimptotájának a grafikon 19

Eltérés 22

Alkalmazása egy eltérés hozzávetőleges számítások 24

A koncepció a különbségek a magasabb rendű 25

Tegyük fel, hogy a függvény az y = f (x) definiált promezhutkeX. Vegyünk egy pont hH. Adunk priraschenieh0 x érték, akkor a függvény kap priraschenieu = f (x + h) -f (x).

A függvény deriváltját y = f (x) nevezzük határa az arány a növekmény funkció a növekmény az érvelés, amikor az utóbbi nullához (ha ez a határérték létezik):.

A származék is nevezzük y „idy / dx.

Geometriai értelmében a származék

Ahhoz, hogy megértsük a geometriai jelentése a származék, úgy a problémát az érintő.

Tekintsünk egy sík grafikon egy folytonos függvény az y = f (x) (lásd. 3.1 ábra).

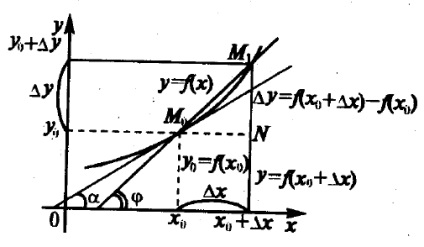
Készítünk egy érintőleges ez a görbe a ponton a M0 (x0. Y0). Először meg kell határozni a fogalmát érintőjének. Ehhez az érv adunk x0 priraschenieh és adja át a görbe y = f (x) a pont a M0 (x0, f (x0)), hogy a pont az M1 (X0 + h, F (X0 + h)). Rajzolj egy kereszteződés M0 M1. Subtangent hogy a görbe y = f (x) megvalósítani a végállás a szelő közelítés M0 M1 M1 egy pont-pont M0. azaz prih0.

Corner vágási M0 M1 faktor (tan uglanaklona ezen a vonalon, hogy az abszcissza) megtalálható izM0 M1 N:

. Aztán a sarokban tangens együttható (tg ugla) jelentése.

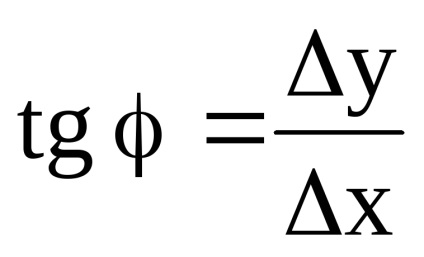
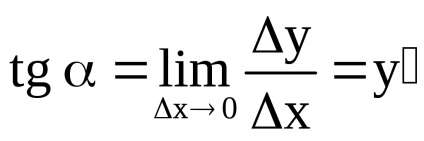
Így a származék a függvény meredeksége az érintő a grafikon az X-tengelyen (tangenciális szögletes együttható).

Fizikai és gazdasági jelentését a származékos

Tekintsünk egy lineáris mozgás a törvény által s = s (t), gdes- áthaladni útját AT- időt. Meg kell találni a sebesség dvizheniyavv momentt0.

Az időintervallum fejeződik ts momentat0 rasstoyanies = s (t0 + t) -s (t0). Ekkor az átlagos sebesség, ez idő alatt sostavits / t. A kevésbé promezhutokt, annál jobb az arány értékelni fogja a sebességet idején vremenit0:

.

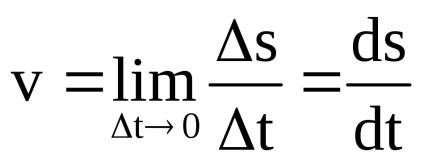
Így a függvény deriváltját a változási sebességének függvény értékei azon a ponton. Ez a jelentés a származék, amelyek nemcsak a fizika, hanem a gazdaságban.

Például, ha a funkció p = p (q) fejezi a függőség a kimeneti pribylipot produktsiiq, ez azt mutatja, származékát marginális profit növekedési (változási sebessége eredmény, amikor a változó termelési):

. Ha funktsiyaq = q (u) fejezi ki a függőség a térfogata proizvodstvaqot rabotnikovu, akkor annak származékát mutatja a változás mértéke a hangerő, ha változtatni az alkalmazottak száma:(Határtermelékenység további dolgozó). Ha a függvény írja le a függőség a termelés az időt megkapjuk a termelékenység az egységnyi idő alatt. Ha funktsiyaw = w (q) fejezi ki függőséget a termelési költségek a termék mennyisége, akkor a származék a határköltség (megközelítőleg mutatja a járulékos költségek további egységének áruk előállítása):Stb

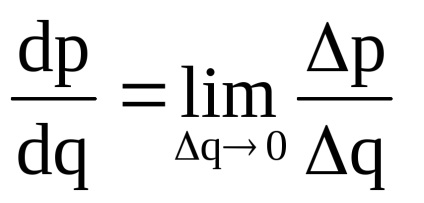
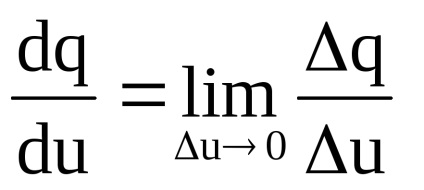
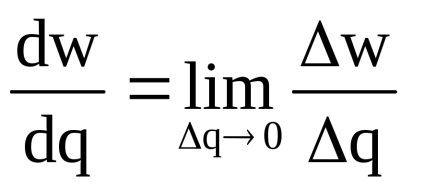
Ennek alapján a koncepció egy származéka határbevétel, marginális bevétel számított a gazdaságban, a marginális termék, határhaszon, marginális termelékenység és egyéb határértékek.

Limit értékek jellemzik a változási folyamat a szervezet. Így, a származék működik változási sebességét az egység (folyamat) idővel, vagy egymáshoz képest a vizsgált tényező.

Kapcsolódó cikkek

• Hogy van a „újságírás” a digitális térben

• A rendszer számítási a származék

• Hogyan épül fel a képet a cég koncepciója „kép” olyan képet, benyomást