A rendszer számítási a származék
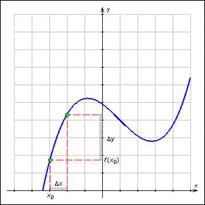
Legyen a függvény y = f (x) meghatározott intervallumban X. Vegyünk egy pontot. Adunk egy x értékét megnöveljük. akkor a függvény értékét megnöveljük.
Definíció. Függvény deriváltját y = f (x) van a határ, hogy az arány a növekmény funkciója a növekmény a független változó nullához az utolsó (ha ez a határérték létezik)
A derivált függvény az úgynevezett differenciálódását ezt a funkciót.
Ha a funkció a ponton x véges-származék, a funkció az úgynevezett differenciálható ezen a ponton.
Funkció differenciálható minden pontján az intervallum X, azt mondta, hogy differenciálható etompromezhutke.
Geometriai értelmében a származék. származék a szögletes együttható (meredekség) tangenciálisan. felhívjuk a görbe y = f (x) a ponton. azaz.
Ezután az egyenlet az érintő a görbe y = f (x) a ponton van a forma
A mechanikus értelmében származék. származék, ahogy az időben a sebesség egy adott időpontban:
A gazdasági jelentését a származék: származéka a kimenő termékeket időben van a termelékenység idején.
A kapcsolat a folytonosság és
differenciálható függvény
Tétel. Ha a függvény az y = f (x) differenciálható a ponton. akkor folyamatosan ezen a ponton.
Kapcsolat tétel hamis, azaz, ha a függvény folytonos ezen a ponton, ez nem feltétlenül differenciálható ezen a ponton.
Ennek egyik példája a függvény y = | x |, folytonos az x = 0, de van egy „megtörés” benne. A származékot ezt a funkciót az x = 0 nem létezik, ettől.
Így a folytonosság a funkció - szükséges, de nem elégséges feltétele differenciálható.
A rendszer számítási a származék
Származékos megtalálható a következőképpen:
1. Adunk egy érv x távolsággal, és megtalálni a felhalmozódott a függvény értékét.
2. Keresse meg a növekmény a funkciót.
3. A komponense kapcsolatok.
4. megtalálják a határa az arány. azaz (ha ez a határérték létezik).
1. példa Find a függvény deriváltját.
1. Adunk egy érv x távolsággal, és megtalálni a felhalmozódott a függvény értékét.
2. Keresse meg a növekmény funkció:
3. A komponense kapcsolatok.
4. Keresse meg a határt
1. A származék állandó nulla :.
2. A származék az érv egyenlő eggyel :.
3. A származék mennyisége összegével egyenlő a származékos ezeket a funkciókat
4. A származék terméket két differenciálható funkciók:
5. A konstans faktorral lehet venni, mint a jele, a származék
6. származéka hányadosa két differenciálható funkció is található a következő képlet:
7. A származék az összetett függvény
Származékai alapvető elemi függvények: