A fraktál elmélet (Part II)
A módszer a „iterált függvény rendszerek” (Iterált funkciók Rendszer - IFS) jelent meg a közepén 80-as, mint egy egyszerű módját jelenti a fraktál struktúrák.
Az IFS olyan funkciót egy fix osztály, és megjelenít egy többdimenziós sor egyéb funkciók. A legegyszerűbb IFS áll affin transzformációk a síkban:
X „= A * X + B * Y + C
Y „= F * X + E * Y + F
Affin transzformáció - a kompozíció egy lineáris transzformáció, és a párhuzamos fordítás. A kétdimenziós térben a teljes képviseletét affin transzformáció elegendő megadni 6 együtthatók.
1988-ban, a híres amerikai szakértő a dinamikai rendszerek elméletében és ergodikus elmélet Barnsley és Sloan felajánlott néhány ötletet megfontolásokon alapuló, a dinamikai rendszerek elméletében, tömörítésére és tárolására képes információt. Úgy hívják, hogy a módszer a módszer fraktál kép tömörítési információkat. A név eredete társított, hogy a geometrikus képek felmerülő ez a módszer általában egy fraktál természetű abban az értelemben, Mandelbrot.
Ezen elgondolás alapján, Barnsley és Sloan létrehozott egy algoritmus, hogy azt állítják, lehetővé teszi információk szorítani 500-1000 alkalommal. Röviden, a módszer leírása a következő. A kép kódolt néhány egyszerű transzformációk (ebben az esetben a affin), azaz ez az átalakulás együtthatók (ebben az esetben az A, B, C, D, E, F).
Például kódolnak egy bizonyos kép a két affin transzformációk, akkor egyértelműen meghatározzák azt a 12 tényező. Ha most kérni minden kezdeti pontot (például X = 0, Y = 0), és indítsa el a iteratív folyamat, az első iteráció után, azt kapjuk, két pont után a második - négy, miután a harmadik - nyolc, stb A néhány tíz ismétléseket adathalmazt pontok leírják a kódolt kép. De a probléma az, hogy nagyon nehéz megtalálni IFS együtthatók, amelyek kódolják egy tetszőleges képet.
A konstrukció az IFS használjuk azzal az eltéréssel affin és más osztályba tartozó egyszerű geometriai transzformációk, amelyek meghatározott kis paraméterek száma. Például, projektív:
X „= (A1 * X + B1 * Y + C1) / (D1 * X + E1 * Y + F1)
Y „= (A2 * X + B2 * Y + C2) / (D2 * X + E2 * Y + F2)
X „= A1 * X * X + B1 * X * Y + C1 * Y * Y + D1 * X + E1 * Y + F1
Y „= A2 * X * X + B2 * X * Y + C2 * Y * Y + D2 * X + E2 * Y + F2
átalakulás a síkban.
Példaként, a használata IFS fraktál struktúrák építeni, úgy a Koch-görbe (1. ábra), és a „sárkány” Harter-Heituey (2. ábra). Mi megkülönböztetni ezeket a struktúrákat, mint a részek, és mindegyikre kiszámolja a affin transzformáció együtthatóit. Az affin kollázs lesz benne, mint az affin transzformációk, mint vannak olyan részei, mint az egész képet.
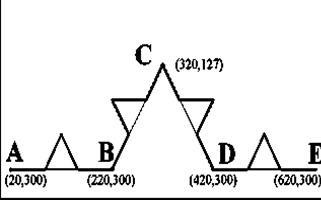
7. ábra előkészítése építési a IFS „sárkány” Harter-Heituey.
IFS megépíteni a "sárkány" Harter-Heituey. Ennek megszervezése első generációs fraktál rács koordináta kijelző 640 x 350 (ábra7). Jelöljük a pont a kapott szaggatott vonal A. B. C. szabályai szerint az építési, ezt a fraktál két részből, mint például a teljes - az 5. ábra egy törött ADB és BEC. Ismerve a koordinátáit a végei ezen szegmensek, akkor ki lehet számítani a együtthatók két affin transzformáció, amely a szaggatott vonal ABC ADB és BEC.
X „= -0.5 * X -0.5 * Y + 490
Y „= 0,5 * X -0.5 * Y + 120
X „= 0,5 * X -0.5 * Y + 340
Y „= 0,5 * X + 0,5 * Y - 110
Mivel egy kezdeti kiindulási pont (például X = 0, Y = 0), és a rá ható iteratív e IFS, miután a tizedik iteráció a képernyőn, így a fraktál szerkezet a 8. ábrán látható, amely a „Sárkány” Harter-Heituey. Ő kód (tömörített leírás) egy sor együtthatók két affin transzformációk.
8. ábra: "Dragon" Harter-Heituey, postpoenny használva IFS a ppyamougolnike 640x350.
Hasonlóképpen, az egyik lehet építeni IFS a Koch-görbe. Könnyen belátható, hogy a görbe négy részből áll, mint az egész görbe. Ahhoz, hogy megtalálja az IFS újra rendezni az első generációs fraktál rács koordináta kijelző 640 x 350 (ábra9).
9. ábra: előkészítése építési IFS Combustion Koch.
Az építési igényel egy sor affin transzformációk, amely négy átalakulások:
X „= 0,333 * X + 13,333
Y „= 0,333 * Y + 200
X „= 0,333 * X + 413,333
Y „= 0,333 * Y + 200
X '= 0,167 * X + 0,289 * Y + 130y' = -0,289 * X + 0,167 * Y + 256
X '= 0,167 * X - 0,289 * Y + 403 Y' = 0,289 * X + 0,167 * Y + 71
Ennek hatása affin kollázs utáni tizedik iteráció látható a 10. ábrán.
10. ábra: Az égés Koch postpoennaya segítségével IFS a ppyamougolnike 640x350.
Használata IFS kompressziós hétköznapi képek (például fényképek) alapul azonosítása helyi önhasonlósággal ellentétben fraktálok, ahol van egy globális önhasonlósági és megállapította IFS nem túl nehéz (mi még csak most láttam ezt). By Barnsley algoritmus megjelent a kép területek a gőz, a kisebbik, amely hasonlít az egyre együtthatók megőrzése kódolás átalakulás, hogy vesz egy nagy terület egy kisebb. Ez megköveteli, hogy több „kisebb” terület teljes képet. Ebben az esetben, a fájl kódoló kép rögzítése nem csak a tényezők, amelyek jellemzik a konverziós eredményeket, hanem a helyét a lineáris méretei a „nagy” területek, amelyek együtt a együtthatók ismertetjük a helyi önhasonlóságának a kódolt kép. Regeneráló algoritmus ebben az esetben is alkalmazni egyes transzformációs nem az egész ponthalmaz elő az előző lépésben az algoritmus, és bizonyos részüket, a régióhoz tartozó megfelelő alkalmazandó átalakulás.
Az egyik legszembetűnőbb példa különböző rendszerek közötti iterált Rui funkciók kétségtelenül nyitva M. Barnsley siste- ma négy nyomó affin transzformációk attraktor, melyek egy sor pontot, feltűnően emlékeztet az alakja egy páfrány levél képet. Leírható a következő táblázatban
Minden sor az ebben a táblázatban megfelel egyetlen, affin transzformáció együtthatóit a, b. c, d. e, f összhangban expressziós
Az utolsó oszlopban a valószínűsége p. miáltal egy véletlen iterációs módszert választjuk a különleges transzformáció.
Az eredmény ez a rendszer funkcióit első becslése a különböző ismétlések számát ábrán látható. 1.43. Meg lehet tekinteni, mint egy növekedés az ismétlések számát valóban

van egy egyre világos képet páfrány levél, meglepően emlékeztet egy meglévő üzem a természetben.
Ez pontok halmaza végtelen önhasonló, mint az várható volt minden fraktál. Amint az ábrából látható. 11, fokozott kis töredékei hasonló képeket az egész. Ahhoz, hogy megoldja ezeket a fragmentumokat csak akkor van szükség, hogy az ismétlések számát is elég nagy.
Így minél használt a felbontás, annál több pontot kell tenni a számítógép memóriájában, hogy megvalósuljon a megfelelő képet. Másrészt, hogy memorizálni a koordinátáit ezeket a pontokat nem szükséges, mivel minden egyes alkalommal, amikor újra lehet előállítani egy rendszer funkciói megegyeznek a táblázat

Ábra. 11. nagyított fragmens páfrány levél
Ennek eredményeként összesen 28 szám tartalmazza az összes szükséges információt erről nem triviális szám! Van egy ötletem, és azt, hogy az ilyen módon nem lehet „kódolva”, és egyéb képek. Ezt az elképzelést gyakorlatba való átültetését, lehetővé tenné, hogy összenyomja a KÉP-sének több tíz vagy akár több száz alkalommal. És valóban, 1988-ban ez sikeresen végrehajtani Barnsley és Sloan kompatibilis okostelefonok általuk létrehozott, de a cég kódolás és a tömörítési grafikus információk a megfelelően kiválasztott a rendszer funkcióit.
A generál fraktál minták írni egy programot algoritmus Pascal, BASIC és más programozási nyelveket. Számos irodalom részletesen megvizsgálták, ahol írt egy programot generáló algoritmus fraktálok, például R. M. Kronover „Káosz és fraktálok a dinamikus rendszerek. Alapjai az elmélet, „a tartalom tárgyalt elmélet a fraktálok, valamint példákat írunk egy programot hozunk létre fraktálok. De ma van a nagy számú már megírt programok fraktálok képeket. Tekintsük egyikük Fractal Explorer 2.02-es verziójával.
Fractal Explorer indításakor megjelenik az üres mezőbe, a tetején van egy eszköztár.
A bal oldali aktív hat ikonok. Az első öt, hogy új, a hatodik nyitni egy korábban mentett. Ha például lenyomva az első ikon elindul generált fraktál Mandelbrot, és akkor jön létre, valós időben. A Méret menüben meg lehet változtatni a felbontást a fraktál kép. Alapértelmezett 300 x 300, a listából az engedélyeket, akkor sem hozzáadni vagy kivonni. Mivel a felbontás által generált fraktál hosszabb, mint korábban, például a számítógépek egyre nehezebb kiszámítani a fraktál több pontot. Ha duplán kattint a bal egérgombbal növeli a fraktál, de ez csak egyre nagyobb és számítják újra. Miután generált fraktál lehet változtatni a paramétereket nektorye fraktál generáció. Megnyomásával megjelenik egy ablak,
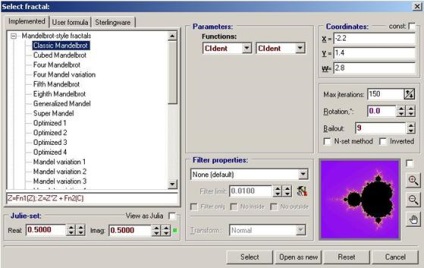
ahol megváltoztathatja az iteratív képlet, az iterációk számát, függvényparaméterek, és sok más beállításokat.
Azt is építeni egy olyan rendszert iterált függvények, ami fraktál páfrány. Alapértelmezésben építeni ezt a fraktál ér 100 ismétléseket. Ha páfrány levél elkezd növekedni, akkor, amikor egy viszonylag kis növekedést is látható, hogy ez áll a pontokat. Amikor változó 100 iteráció 5000, egy kinagyított részletét egy páfrány levél már sokaságából áll, a páfrány levelek.
Végén a leírás a program Fractal Explorer, azt lehet mondani, hogy ez nagyon érdekes látni, akkor hogyan húzott fraktál, a paletta amilyennek festik. Erősen kívánt fraktál, mentheti vagy nyomtatásban.
Talán új ötletek fraktálgeometriai a jövőben segíteni fog felfedezni a sok rejtélyes természeti jelenség.
Jelenleg fraktálok és multifraktáloknál gyorsan behatolnak számos területen a fizika. Fractal módszerek képfeldolgozás és alakfelismerés segítségével új koncepciók segítségével a kutatók, hogy alkalmazza a matematikai apparátus kvantitatív leírását hatalmas természeti tárgyak és szerkezetek.