Mágikus funkciók és integrál
Szia kedves egyetemisták Argemony! Jó látni, hogy a következő előadás mágikus funkcióit és integrál.
Ma már a napirenden - oktatás, először is, a mágikus egy parabola. Itt fogjuk kezdeni.
Az általános formája a parabola (másodfokú függvény)
Az együtthatók b és c értéke nullával egyenlő (egyidejűleg vagy nem), de az együttható „a” nulla nem lehet, különben nem lesz egy másodfokú függvénnyel.
A legegyszerűbb funkció egy parabola formában van
Látjuk, hogy a jellemzői ennek a függvény nem rendelkezik. Ennélfogva domén a teljes szám vonal (-∞; + ∞), és a beállított értékek - csak nemnegatív része a vonal [0; + ∞).
És most mi használ a megszerzett ismereteket a korábbi leckéket, próbálkozzon magic megváltoztatni az együtthatók a mágikus funkciót.
Hozzáadása az együttható „a”, kivéve az 1. változásához vezet az amplitúdó a parabola ágak. Ha | a |> 1, akkor a parabola keskenyebb lesz, és ha | a |<1, то ветви расходятся в стороны и парабола становится шире.
Most tekintsünk egy ilyen funkció
Hozzáadása az állandó „c”, mint egy kifejezés, hogy kifejezze egy négyzet parabola vezet mozgását felfelé vagy lefelé a „c” pozíciókat. Ennek megfelelően változik a beállított értékek a funkciót.
Nos, most már sejthetjük, hogy a rendelkezés ugyanis a bx, nyilván, vezet az elmozdulás a vízszintes parabola.
Vizsgáljuk meg ezt a pontot részletesebben. Próbáljuk azonosítani szempontjából (1) egy teljes négyzet. Sőt, ha van számszerű koefficiensek az egyenlet, minden sokkal világosabb, úgyhogy lépni numerikus együtthatók levél:
a = 2; b = 4; c = 5
y = 2x 2 + 4x + 5 = 2 (x + 1) 2 +3
Most óvatosan elkezdi szétszerelni a varázsa ennek másodfokú függvény. Kezdjük belülről.
Látjuk, hogy x nem tér, és (x + 1). Az előző órák, emlékezünk, hogy az együttható távú közel x mágikus jobbra funkció vízszintesen balra vagy jobbra. Ebben az esetben az 1 egység a bal oldalon.
Következő, figyeljen aránya körülbelül 2 négyzetméter. Ő összenyomódik a mágikus egy parabola. Ez lesz keskenyebb. Ha ez az arány még mindig negatív, akkor a parabola kell fordítani 180 fokkal, és az ágak válna lenézni.
Továbbá, az akció belép az együttható 3, és alkalmazza a mágikus okozó mozgás parabola legfeljebb 3 db.
Feladat 1. Minden veszi parabola (1).
Az együtthatók meghatározása a következő:
a = az első szám a szobában az LD
b = a második szám a szobában az LD
c = a harmadik szám a szobában az LD vagy a-b, ha a kétjegyű szám az LD.
Meg kell vizsgálni ezt a példázatot, ahogy tettük az osztályban, megjegyezve rések és csökkenő vagy növekvő.
A tanulság még nincs vége. Menjünk tovább. A helyzet a parabola a koordinátatengelyek függ az együtthatók a, b, c.
A megjelölés az együttható a függvénye, mint irányított parabola ágak:
ha a> 0, akkor a parabola ága felfelé;
ha egy<0, то ветви параболы направлены вниз.
Azt hiszem, emlékszem, hogyan kérik a gyökerei egy másodfokú egyenlet megfelelő másodfokú függvényt,
Igen, a számítás a diszkrimináns. Roots lehet 2, előfordulhat, hogy egy (sőt 2 gyökerek, de azok azonosak), vagy a root. De nincs igazi gyökereit, de a képzeletbeli gyökereket, hanem ezeket a gyökereket, azt mondjuk, hogy nem fog, de feltárják még érdekesebb varázslat, de erről később. sokkal később. Ha érdekli ez, aztán vissza a gyökerekhez, és a képzeletbeli mágikus függvények a komplex változó. Mágiáját még inkább hihetetlen, és meg tudja csinálni, mint a csodák, hogy sokan nem is álmodott. De most már csak beszélni a valódi gyökerei a másodfokú egyenlet.
Tehát, ha a gyökerek 2, az azt jelenti, hogy a parabola keresztezi az x tengelyen a két pontot.
Ha az egyik gyökérben (vagy inkább a kettő ugyanaz), ez azt jelenti, hogy a parabola érinti az x-tengely ugyanazon a ponton.
Ha a diszkriminánsa másodfokú egyenlet, amely megfelel egy másodfokú függvény negatív, akkor az egész parabola vagy fölött van OX, vagy alatta.
Ismét felhívom a figyelmet arra a tényre, hogy a domain a parabola az egész valós tengelyen, hanem olyan értékrendet helyzetétől függ a parabola.
Feladat 2. Ezekben a grafikonok nekem, tekintve a skála a 1: 1, írja be az értékrend az összes funkció 1-6.
És most a gyors pillantást az általános formája a hálózati funkció
y = x n. n-természetes szám (4)
Nyilvánvaló, hogy amikor az N-páros szám, a forma a funkció hasonló az (1).
Ha n-páratlan szám, a függvény grafikon megszűnik páros, páratlan, és ez lesz a feltétel F (-x) = - f (x). Ez a funkció típusát is nevezik harmadfokú parabola.
3. A keresés Cél domén és a beállított értékeket a függvény (4) a különböző n- (páros és páratlan).
És végül, az utolsó. Tekintsük a inverz függvény (4). Mi művelet fordított hatványozást? Természetesen a gyökér kivonatot.
Itt is meg kell vizsgálni a két esetben.
1. n-is. A doménje meghatározás - nemnegatív tengely [0; + ∞), mert egy negatív szám nem lehet eltávolítani még a gyökerét.
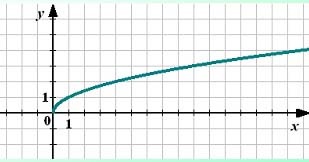
2. N - páratlan. A grafikon a formája
4. Cél megadása a funkció (5) és több tartomány értékeket. Összehasonlítása grafikonok funkciók (4) és (5).
És a végén fogom mutatni, hogyan kell építeni grafikonok inverz függvények. A grafikonok inverz függvények szimmetrikus a felezővonal 1. és 3. negyedre. Ezért, hogy tartsa a vonalat, és elég tükrözik szimmetrikusan menetrendjét hatalmi funkciót.
Az ábra képviseltem mindkét esetben teljesítmény funkciók és visszatérni. Amint látjuk, abban az esetben n-páratlan rendben: a két ág szimmetrikusan tükröződik felezővonal és fogadása funkciót. De abban az esetben n-egy még az egyik ág húzott szaggatott, mert nem szerepel a függvény grafikonját, úgy, hogy az eredményül kapott görbe szimmetrikus reflexió funkció nem.
Probléma, hogy 5. megjelenítése ha mi is ágat, és berohant a menetrend, akkor a menetrend nem működik.
Küldje munka révén FIÓKOM
Kérdések nyugodtan át a Perszephoné
A legjobb ajánlat a szalonban jaguár xj a hivatalos forgalmazótól.